题目内容
9. 如图,A,B两处加工厂需从设在x轴上的C贷站和y轴上的D货站来回调运货物,当C,D建于何处时,AB+BC+CD+DA的路程最短?
如图,A,B两处加工厂需从设在x轴上的C贷站和y轴上的D货站来回调运货物,当C,D建于何处时,AB+BC+CD+DA的路程最短?
分析 根据轴对称的性质分别作出B关于x轴的对称点B′,作A关于y轴的对称点A′,连接A′B′交x轴于C,交y轴于D,即可得到结论.
解答  解:如图所示,
解:如图所示,
作B关于x轴的对称点B′,作A关于y轴的对称点A′,连接A′B′交x轴于C,交y轴于D,
则AB+BC+CD+DA的路程最短.
点评 本题考查了轴对称的性质-最短路线问题,作图与应用设计作图,熟练掌握两点之间线段最短的性质是解题的关键.

练习册系列答案
相关题目
20.|1-tan45°|的值为( )
| A. | $\frac{1}{2}$ | B. | 1-$\frac{{\sqrt{2}}}{2}$ | C. | 1-$\frac{{\sqrt{3}}}{2}$ | D. | 0 |
9.点P是图①中三角形边上一点,坐标为(a,b),图①经过变化形成图②,则点P在图②中的对应点P′的坐标为( )
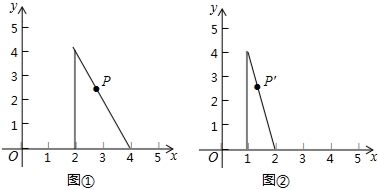

| A. | ($\frac{1}{2}$a,$\frac{1}{2}$b) | B. | ($\frac{1}{2}$a,b) | C. | (a-2,b) | D. | (a-1,b) |
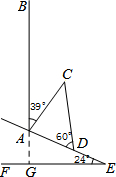 如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.
如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.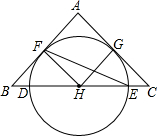 如图,在△ABC中,AB=AC,BC经过⊙H的圆心交⊙H于点D、E,AB、AC是圆的切线,F、G是切点.
如图,在△ABC中,AB=AC,BC经过⊙H的圆心交⊙H于点D、E,AB、AC是圆的切线,F、G是切点.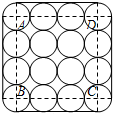 如图是一个组合烟花的横截面,其中16个圆的半径相同,点A、B、C、D分别是四个角上的圆的圆心,且四边形ABCD为正方形.若圆的半径为r,则组合烟花截面的周长和面积分别是多少?
如图是一个组合烟花的横截面,其中16个圆的半径相同,点A、B、C、D分别是四个角上的圆的圆心,且四边形ABCD为正方形.若圆的半径为r,则组合烟花截面的周长和面积分别是多少?