题目内容
5.某超市设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“5元”、“10元”、“20元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回),并根据两个小球所标总金额换取等值的购物券.某顾客刚好消费200元,则该顾客所获得购物券的金额不低于20元的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
分析 列表法或画树状图得到所有可能的结果,再找到该顾客所获得购物券的金额不低于20元的情况数,即可求出其概率.
解答 解:列表:
| 第二次 第一次 | 0 | 5 | 10 | 20 |
| 0 | -- | 5 | 10 | 20 |
| 5 | 5 | -- | 15 | 25 |
| 10 | 10 | 15 | -- | 30 |
| 20 | 20 | 25 | 30 | -- |
因此P(不低于20元)=$\frac{6}{12}$=$\frac{1}{2}$.
故选A.
点评 本题主要考查用列表法或树状图求概率.解决本题的关键是弄清题意,满200元可以摸两次,但摸出一个后不放回,概率在变化.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
15.已知圆锥的侧面积为6πcm2,侧面展开图的圆心角为60°,则该圆锥的母线长( )
| A. | 36cm | B. | 18cm | C. | 6cm | D. | 3cm |
16.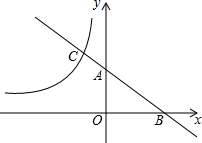 如图,平面直角坐标系中,直线y=-x+a与x、y轴的正半轴分别交于点B和点A,与反比例函数y=-$\frac{3}{x}$的图象交于点C,若BA:AC=2:1,则a的值为( )
如图,平面直角坐标系中,直线y=-x+a与x、y轴的正半轴分别交于点B和点A,与反比例函数y=-$\frac{3}{x}$的图象交于点C,若BA:AC=2:1,则a的值为( )
 如图,平面直角坐标系中,直线y=-x+a与x、y轴的正半轴分别交于点B和点A,与反比例函数y=-$\frac{3}{x}$的图象交于点C,若BA:AC=2:1,则a的值为( )
如图,平面直角坐标系中,直线y=-x+a与x、y轴的正半轴分别交于点B和点A,与反比例函数y=-$\frac{3}{x}$的图象交于点C,若BA:AC=2:1,则a的值为( )| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
20.|1-tan45°|的值为( )
| A. | $\frac{1}{2}$ | B. | 1-$\frac{{\sqrt{2}}}{2}$ | C. | 1-$\frac{{\sqrt{3}}}{2}$ | D. | 0 |
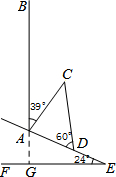 如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.
如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.