题目内容
2.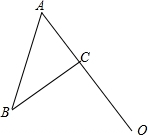 如图,在△ABC中,AB=5,BC=4,AC=3,点O在AC的延长线上,且OC=4.
如图,在△ABC中,AB=5,BC=4,AC=3,点O在AC的延长线上,且OC=4.(1)试作出△ABC关于点O成中心对称的△A′B′C′;
(2)连接A′B,AB′,则四边形ABA′B′是中心对称图形吗?
(3)试求四边形ABA′B′的面积.
分析 (1)作出△ABC及点O,然后找出点A、B、C关于点O的对称点A′、B′、C′,然后顺次连接即可.
(2)与证明四边形ABA′B′是中心对称图形,只需推知四边形ABA′B′是平行四边形即可.
(3)根据S平行四边形ABA′B′=2S△AA′B计算即可.
解答 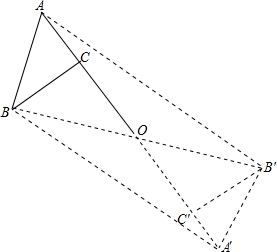 解:(1)如图所示,△A′B′C′即为所求的三角形.
解:(1)如图所示,△A′B′C′即为所求的三角形.
(2)结论:四边形ABA′B′是中心对称图形.
理由如下:∵∠BAA′=∠B′A′A,
∴AB∥A′B′,又∵AB=A′B′,
∴四边形ABA′B′是平行四边形,
∴四边形ABA′B′是中心对称图形.
(3)∵四边形ABA′B′是平行四边形,
∴S平行四边形ABA′B′=2S△AA′B,AO=OA′=7,AA′=14
∵AB=5,BC=4,AC=3,
∴AB2=BC2+AC2,
∴△ACB是直角三角形,
∴∠BCA=90°即BC⊥CA,
∴S平行四边形ABA′B′=2S△AA′B=2×$\frac{1}{2}$×14×4=56.
点评 本题考查作图旋转变换、平行四边形的判定、平行四边形的面积等知识,理解中心对称的定义是解决问题的关键,记住平行四边形的对角线把平行四边形分成两个全等三角形,这两个三角形面积相等,属于中考常考题型.

练习册系列答案
相关题目
 已知,在△ABC中∠ACB=90°,AC=BC,点P在△ABC内,且PA=3,PB=1,PC=2,求证:∠BPC=135°.
已知,在△ABC中∠ACB=90°,AC=BC,点P在△ABC内,且PA=3,PB=1,PC=2,求证:∠BPC=135°.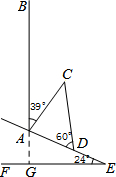 如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.
如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.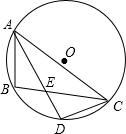 如图,AB,AC是⊙O弦,∠BAC的角平分线交⊙O于点D,AD与BC交于点E,若DE=2cm,AE=8cm,则DC=2$\sqrt{5}$cm.
如图,AB,AC是⊙O弦,∠BAC的角平分线交⊙O于点D,AD与BC交于点E,若DE=2cm,AE=8cm,则DC=2$\sqrt{5}$cm.