题目内容
11.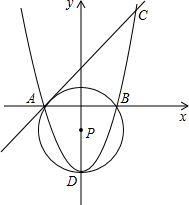 在平面直角坐标系中,已知点A(-2,0),B(2,0),C(3,5).
在平面直角坐标系中,已知点A(-2,0),B(2,0),C(3,5).(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;
(2)求过点A,B及抛物线的顶点D的⊙P的圆心P的坐标;
(3)在抛物线上是否存在点Q,使AQ与⊙P相切,若存在请求出Q点坐标.
分析 (1)利用抛物线和x轴的两个交点坐标,设出抛物线的解析式y=a(x-x1)(x-x2),代入即可得出抛物线的解析式,再设出直线AC的解析式,利用待定系数法即可得出答案;
(2)先求得抛物线的顶点D的坐标,再设点P坐标(0,Py),根据A,B,D三点在⊙P上,得PB=PD,列出关于Py的方程,求解即可得出P点的坐标;
(3)假设抛物线上存在这样的点Q使直线AQ与⊙P相切,设Q点的坐标为(m,m2-4),根据平面内两点间的距离公式,即可得出关于m的方程,求出m的值,即可得出点Q的坐标.
解答  解:(1)∵A(-2,0),B(2,0);
解:(1)∵A(-2,0),B(2,0);
∴设二次函数的解析式为y=a(x-2)(x+2)…①,
把C(3,5)代入①得a=1;
∴二次函数的解析式为:y=x2-4;
设一次函数的解析式为:y=kx+b(k≠0)…②
把A(-2,0),C(3,5)代入②得$\left\{\begin{array}{l}-2k+b=0\\ 3k+b=5\end{array}\right.$,
解得$\left\{\begin{array}{l}k=1\\ b=2\end{array}\right.$,
∴一次函数的解析式为:y=x+2;
(2)设P点的坐标为(0,Py),
由(1)知D点的坐标为(0,-4);
∵A,B,D三点在⊙P上;
∴PB=PD;
∴22+Py2=(-4-Py)2,
解得:Py=-$\frac{3}{2}$;
∴P点的坐标为(0,-$\frac{3}{2}$);
(3)在抛物线上存在这样的点Q使直线AQ与⊙P相切.
理由如下:设Q点的坐标为(m,m2-4);
根据平面内两点间的距离公式得:AQ2=(m+2)2+(m2-4)2,PQ2=m2+(m2-4+$\frac{3}{2}$)2;
∵AP=$\frac{5}{2}$,
∴AP2=$\frac{25}{4}$;
∵直线AQ是⊙P的切线,
∴AP⊥AQ;
∴PQ2=AP2+AQ2,
即:m2+(m2-4+$\frac{3}{2}$)2=$\frac{25}{4}$+[(m+2)2+(m2-4)2]
解得:m1=$\frac{10}{3}$,m2=-2(与A点重合,舍去)
∴Q点的坐标为($\frac{10}{3}$,$\frac{64}{9}$).
点评 本题考查了二次函数的综合题,涉及的知识点还有利用待定系数法求一次函数的解析式和二次函数的解析式,一元二次方程,是一道综合性较强的题目,但难度不大,要熟练掌握解题思路和方法.

 新思维寒假作业系列答案
新思维寒假作业系列答案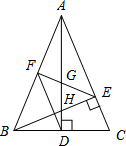 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确的有( )
如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确的有( )| A. | 1个 | B. | 2 个 | C. | 3 个 | D. | 4个 |
| A. | $x>-\frac{2}{3}$ | B. | $x<-\frac{2}{3}$ | C. | $x>-\frac{3}{2}$ | D. | $x<-\frac{3}{2}$ |
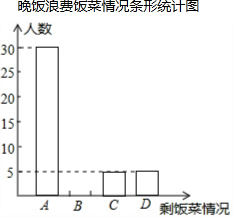 自从2012年12月4日中央公布“八项规定”以来,某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据统计结果绘制了如下不完整的统计图表,根据所提供的信息回答下列问题:
自从2012年12月4日中央公布“八项规定”以来,某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据统计结果绘制了如下不完整的统计图表,根据所提供的信息回答下列问题:晚饭浪费饭菜情况统计表
| 选项 | 频数 | 频率 |
| A | 30 | m |
| B | n | 20% |
| C | 5 | 10% |
| D | 5 | 10% |
(2)请把“晚饭浪费饭菜条形统计图”补充完整;
(3)若绘制““晚饭浪费饭菜条形统计图””,调查内容为“饭吃完但菜有剩”所对应的圆心角等于36度
(4)该中学有学生2200名,请估计这餐晚饭中“有饭吃但菜吃完”和“饭吃完但菜有剩”的学生有660人.