题目内容
17．一项“过关游戏”规定：在过第n关时要将一颗质地均匀的骰子（六个面上分别刻有1到6的点数）抛掷n次，若n次抛掷所出现的点数之和大于n2，则算过关；否则不算过关，则能过第二关的概率是（ ）| A． | $\frac{15}{18}$ | B． | $\frac{5}{18}$ | C． | $\frac{11}{18}$ | D． | $\frac{9}{18}$ |
分析 画树状图展示所有36种等可能的结果数，再找出出现的点数之和大于4的结果数，然后根据概率公式求解．
解答 解：画树状图为：
共有36种等可能的结果数，其中出现的点数之和大于4的结果数为30，
所以能过第二关的概率=$\frac{30}{36}$=$\frac{15}{18}$．
故选A．
点评 本题考查了列表法与树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．
练习册系列答案
孟建平名校考卷系列答案
相关题目
如图，在△ABC中，AB=AC，点D、E分别在BC、AC上，且DC=DE．
12．
如图所示，直线m∥n，则∠α为（ ）
如图所示，直线m∥n，则∠α为（ ）| A． | 70° | B． | 55° | C． | 50° | D． | 30° |
2．
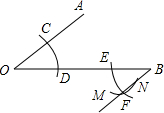如图，用尺规作出了BF∥OA，作图痕迹中，弧MN是（ ）
如图，用尺规作出了BF∥OA，作图痕迹中，弧MN是（ ）| A． | 以B为圆心，OD长为半径的弧 | B． | 以C为圆心，CD长为半径的弧 | ||
| C． | 以E为圆心，DC长为半径的弧 | D． | 以E为圆心，OD长为半径的弧 |
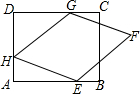如图，矩形ABCD中，AD=6，DC=8，菱形EFGH的三个顶点E、G、H分別在矩形ABCD的边AB、CD、DA上，AH=2．
如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连接AE，F为AE上一点，且∠BFE=∠C．