题目内容
 如图,已知点B(1,-2)是⊙O上一点,过点B作⊙O的切线交x轴于点A,则tan∠BAO=
如图,已知点B(1,-2)是⊙O上一点,过点B作⊙O的切线交x轴于点A,则tan∠BAO=考点:切线的性质,坐标与图形性质
专题:
分析:过点B作BC⊥x轴于点C.故∠COB+∠OBC=90°,点B(1,-2)所以OC=1,BC=2.由切线的性质得∠OBA=90°,∠COB+∠BAO=90°,故∠BAO=∠OBC,tan∠BAO=tan∠OBC=
=
.
| OC |
| OB |
| 1 |
| 2 |
解答:解:过点B作BC⊥x轴于点C.

∴∠COB+∠OBC=90°.
∵点B(1,-2),
∴OC=1,BC=2.
∵AB是⊙O的切线,
∴∠OBA=90°;
∴∠COB+∠BAO=90°,
∴∠BAO=∠OBC,
∴tan∠BAO=tan∠OBC=
=
.

∴∠COB+∠OBC=90°.
∵点B(1,-2),
∴OC=1,BC=2.
∵AB是⊙O的切线,
∴∠OBA=90°;
∴∠COB+∠BAO=90°,
∴∠BAO=∠OBC,
∴tan∠BAO=tan∠OBC=
| OC |
| OB |
| 1 |
| 2 |
点评:本题主要考查了切线的性质以及点的坐标、锐角三角函数的求法.作出辅助线得出∠BAO=∠OBC是解题的关键.

练习册系列答案
相关题目
 如图,从观察点A处发现北偏东45°方向,距离为9
如图,从观察点A处发现北偏东45°方向,距离为9 小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图所示,樱桃单价w(单位:元/kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系.
小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图所示,樱桃单价w(单位:元/kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系.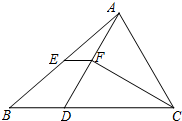 如图,△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
如图,△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.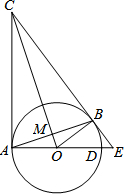 如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E. AB、CO交于点M,连接OB.
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E. AB、CO交于点M,连接OB. 如图,已知函数y=
如图,已知函数y= 如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,线段EF过矩形对角线AC的中点O,且EF⊥AC,PF∥AC,则EF:PE的值是
如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,线段EF过矩形对角线AC的中点O,且EF⊥AC,PF∥AC,则EF:PE的值是