题目内容
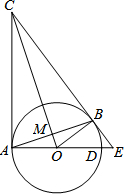 如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E. AB、CO交于点M,连接OB.
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E. AB、CO交于点M,连接OB.(1)求证:∠ABO=
| 1 |
| 2 |
(2)若sin∠EAB=
| ||
| 10 |
| BE |
| AE |
考点:切线的性质,相似三角形的判定与性质,解直角三角形
专题:
分析:(1)由切线长定理及切线的性质得CA=CB,∠BCO=
∠ACB,∠CBO=90°,CO⊥AB于是得∠ABO=∠BCO,所以∠ABO=
∠ACB;
(2)由半径相等得∠EAB=∠ABO,所以∠BCO=∠EAB,sin∠BCO=sin∠EAB=
,求得OB=4即⊙O 的半径为4;再由△OBE∽△CAE得
=
.因为
CA=CB=12,所以
=
.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由半径相等得∠EAB=∠ABO,所以∠BCO=∠EAB,sin∠BCO=sin∠EAB=
| ||
| 10 |
| BE |
| AE |
| OB |
| CA |
CA=CB=12,所以
| BE |
| AE |
| 1 |
| 3 |
解答:(1)证明:∵CA、CB为⊙O的切线,
∴CA=CB,∠BCO=
∠ACB,
∴∠CBO=90°.
∴CO⊥AB.
∴∠ABO+∠CBM=∠BCO+∠CBM=90°.
∴∠ABO=∠BCO.
∴∠ABO=
∠ACB.
(2)解:∵OA=OB,
∴∠EAB=∠ABO.
∴∠BCO=∠EAB.
∵sin∠BCO=sin∠EAB=
.
∴
=
.
∵CB=12,
∴OB=4.
即⊙O 的半径为4.
∴∠OBE=∠CAE=90°,∠E=∠E,
∴△OBE∽△CAE.
∴
=
.
∵CA=CB=12,
∴
=
.
∴CA=CB,∠BCO=
| 1 |
| 2 |
∴∠CBO=90°.
∴CO⊥AB.
∴∠ABO+∠CBM=∠BCO+∠CBM=90°.
∴∠ABO=∠BCO.
∴∠ABO=
| 1 |
| 2 |
(2)解:∵OA=OB,
∴∠EAB=∠ABO.
∴∠BCO=∠EAB.
∵sin∠BCO=sin∠EAB=
| ||
| 10 |
∴
| OB |
| CB |
| 1 |
| 3 |
∵CB=12,
∴OB=4.
即⊙O 的半径为4.
∴∠OBE=∠CAE=90°,∠E=∠E,
∴△OBE∽△CAE.
∴
| BE |
| AE |
| OB |
| CA |
∵CA=CB=12,
∴
| BE |
| AE |
| 1 |
| 3 |
点评:本题主要考查了切线的性质、相似三角形的判定与性质以及解直角三角形.本题综合性较强.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目


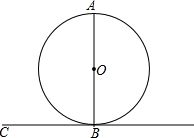 如图,AB是圆O的直径,直线BC与圆O相切于点B.
如图,AB是圆O的直径,直线BC与圆O相切于点B. 如图,已知点B(1,-2)是⊙O上一点,过点B作⊙O的切线交x轴于点A,则tan∠BAO=
如图,已知点B(1,-2)是⊙O上一点,过点B作⊙O的切线交x轴于点A,则tan∠BAO= 如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=
如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=