题目内容
 如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,线段EF过矩形对角线AC的中点O,且EF⊥AC,PF∥AC,则EF:PE的值是
如图,矩形ABCD中,AD=2AB,E、F分别是AD、BC上的点,线段EF过矩形对角线AC的中点O,且EF⊥AC,PF∥AC,则EF:PE的值是考点:矩形的性质,线段垂直平分线的性质,勾股定理
专题:
分析:连接AF,根据线段垂直平分线上的点到两端点的距离相等可得AF=FC,设AB=4a,BF=x,然后表示出AF=8a-x,在Rt△ABF中,利用勾股定理列出方程求出x,再根据相似三角形对应边成比例列式求出AP,然后利用勾股定理列式求出PE、EF,再求出比值即可.
解答: 解:如图,连接AF,
解:如图,连接AF,
∵EF⊥AC,O是AC的中点,
∴EF垂直平分AC,
∴AF=FC,
设AB=4a,BF=x,
∵AD=2AB=2•4a=8a,
∴BC=8a,
AF=FC=8a-x,
在Rt△ABF中,AB2+BF2=AF2,
即(4a)2+x2=(8a-x)2,
解得x=3a,
∴FC=5a,
∵PF∥AC,
∴△ABC∽△PBF,
∴
=
,
即
=
,
解得PB=
a,
∴AP=4a-
a=
a,
易得△AEO≌△CFO,
∴AE=FC=5a,
在Rt△APE中,由勾股定理得,PE=
=
a,
又EF=
=2
a,
∴EF:PE=2
a:
a=
.
故答案为:
.
 解:如图,连接AF,
解:如图,连接AF,∵EF⊥AC,O是AC的中点,
∴EF垂直平分AC,
∴AF=FC,
设AB=4a,BF=x,
∵AD=2AB=2•4a=8a,
∴BC=8a,
AF=FC=8a-x,
在Rt△ABF中,AB2+BF2=AF2,
即(4a)2+x2=(8a-x)2,
解得x=3a,
∴FC=5a,
∵PF∥AC,
∴△ABC∽△PBF,
∴
| PB |
| AB |
| BF |
| BC |
即
| PB |
| 4a |
| 3a |
| 8a |
解得PB=
| 3 |
| 2 |
∴AP=4a-
| 3 |
| 2 |
| 5 |
| 2 |
易得△AEO≌△CFO,
∴AE=FC=5a,
在Rt△APE中,由勾股定理得,PE=
(
|
5
| ||
| 2 |
又EF=
| (4a)2+(8a-2×3a)2 |
| 5 |
∴EF:PE=2
| 5 |
5
| ||
| 2 |
| 4 |
| 5 |
故答案为:
| 4 |
| 5 |
点评:本题考查了矩形的性质,线段垂直平分线上的点到两端点的距离相等的性质,勾股定理,相似三角形的判定与性质,设未知数分别表示出PE、EF是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0035千克污染物.以下是相关的统计图、表:
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0035千克污染物.以下是相关的统计图、表:
 如图,已知点B(1,-2)是⊙O上一点,过点B作⊙O的切线交x轴于点A,则tan∠BAO=
如图,已知点B(1,-2)是⊙O上一点,过点B作⊙O的切线交x轴于点A,则tan∠BAO= 如图,点A在函数y=
如图,点A在函数y= 如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=
如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=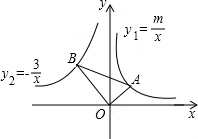 如图,在平面直角坐标系中,∠OAB=60°,∠AOB=90°,反比例函数y1=
如图,在平面直角坐标系中,∠OAB=60°,∠AOB=90°,反比例函数y1=