题目内容
 如图,从观察点A处发现北偏东45°方向,距离为9
如图,从观察点A处发现北偏东45°方向,距离为9| 2 |
| 3 |
(1)点B和点C相距多少海里?
(2)缉私船沿什么方向行驶,才能在最短的时间内追上走私船?并求出所需时间.(参考数据:sin53°≈
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 3 |
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)先解Rt△ABE,得出BE=
AB=9,再解Rt△ACE,得出CE=AE•tan53°=12,然后根据BC=CE+BE即可求解;
(2)设最短经过x小时缉私船在D点追上走私船,则CD=50
x,BD=50x,作DF⊥CB的延长线于F.先解Rt△DBF,得出BF=25x,DF=25
x,则DF=
CD,得出∠DCF=30°,CF=
DF,由此列出方程21+25x=
×25
x,解方程即可.
| ||
| 2 |
(2)设最短经过x小时缉私船在D点追上走私船,则CD=50
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
解答:解:(1)Rt△ABE中,∠BAE=45°,
∴BE=AE=
AB=
×9
=9.
Rt△ACE中,∠CAE=53°,
∴CE=AE•tan53°=9×
=12,
∴BC=CE+BE=12+9=21(海里).
答:点B和点C相距21海里;
 (2)设最短经过x小时缉私船在D点追上走私船,则CD=50
(2)设最短经过x小时缉私船在D点追上走私船,则CD=50
x,BD=50x,作DF⊥CB的延长线于F.
在Rt△DBF中,∠DBF=60°,
∴BF=25x,DF=25
x,
∴DF=
CD,
∴∠DCF=30°,
∴CF=
DF,即
21+25x=
×25
x,
解得x=0.42.
答:缉私船沿北偏东60°方向行驶,最短最短经过0.42小时追上走私船.
∴BE=AE=
| ||
| 2 |
| ||
| 2 |
| 2 |
Rt△ACE中,∠CAE=53°,
∴CE=AE•tan53°=9×
| 4 |
| 3 |
∴BC=CE+BE=12+9=21(海里).
答:点B和点C相距21海里;
 (2)设最短经过x小时缉私船在D点追上走私船,则CD=50
(2)设最短经过x小时缉私船在D点追上走私船,则CD=50| 3 |
在Rt△DBF中,∠DBF=60°,
∴BF=25x,DF=25
| 3 |
∴DF=
| 1 |
| 2 |
∴∠DCF=30°,
∴CF=
| 3 |
21+25x=
| 3 |
| 3 |
解得x=0.42.
答:缉私船沿北偏东60°方向行驶,最短最短经过0.42小时追上走私船.
点评:此题考查了解直角三角形的应用-方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
一次函数y=kx+b与反比例函数y=
,x与y的对应值如下表:不等式kx+b<
的解为( )
| m |
| x |
| m |
| x |
| x | -3 | -2 | -1 | 1 | 2 | 3 | ||||||
| y=kx+b | 4 | 3 | 2 | 0 | -1 | -2 | ||||||
y=
|
|
1 | 2 | -2 | -1 | -
|
| A、x<-1或0<x<2 |
| B、-1<x<0或x>2 |
| C、x>-1或x<2 |
| D、以上答案都不对 |
 在“体育中考”的某次模拟测试中,某校某班10名学生测试成绩统计如图.对于这10名学生的参赛成绩,下列说法中错误的是( )
在“体育中考”的某次模拟测试中,某校某班10名学生测试成绩统计如图.对于这10名学生的参赛成绩,下列说法中错误的是( )| A、众数是28 |
| B、中位数是28 |
| C、平均数是27.5 |
| D、极差是8 |
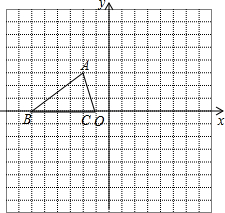 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
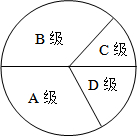 为了解我县1600名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
为了解我县1600名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下: 据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0035千克污染物.以下是相关的统计图、表:
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0035千克污染物.以下是相关的统计图、表: 如图,已知点B(1,-2)是⊙O上一点,过点B作⊙O的切线交x轴于点A,则tan∠BAO=
如图,已知点B(1,-2)是⊙O上一点,过点B作⊙O的切线交x轴于点A,则tan∠BAO=