题目内容
12.已知函数y=x2+mx+m-2的图象与x轴有两个不同的交点.(1)求m的取值范围;
(2)若抛物线与y轴交于点(0,1),求方程x2+mx+m-2=0的两根.
分析 (1)先计算出判别式的值得到△=(m-2)2+4,由于m无论为何实数,△>0,于是得到m的取值范围为全体实数;
(2)把(0,1)代入抛物线解析式得到m=3,然后计算函数值为0时自变量的值即可得到方程x2+mx+m-2=0的两根.
解答 解:(1)根据题意得△=m2-4(m-2)=(m-2)2+4,
∵(m-2)2+4>0,
∴m无论为何实数,△>0,
∴m的取值范围为全体实数;
(2)∵抛物线与y轴交于点(0,1),
∴m-2=1,解得m=3,
∴抛物线解析式为y=x2+3x+1,
当y=0时,x2+3x+1,解得x1=$\frac{-3+\sqrt{5}}{2}$,x2=$\frac{-3-\sqrt{5}}{2}$,
即方程x2+mx+m-2=0的两根为x1=$\frac{-3+\sqrt{5}}{2}$,x2=$\frac{-3-\sqrt{5}}{2}$.
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题可化为解关于x的一元二次方程;△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
17.小明等同学做投掷硬币试验,当他们投掷20次时,发现有7次正面朝上,13次正面朝下,假如他们做这样的试验达到10000次,请你估计硬币正面朝上的频率可能为( )
| A. | 在5000左右附近 | B. | 在7000左右附近 | C. | 在3500左右附近 | D. | 在7500以上 |
 已知如图,线段AB的长为4,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作得等腰直角三角形ACD和等腰直角三角形BCE,
已知如图,线段AB的长为4,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作得等腰直角三角形ACD和等腰直角三角形BCE, 已知,如图,AB⊥BD,ED⊥BD,垂足分别为B、D,求证:AC:EC=BC:DC.
已知,如图,AB⊥BD,ED⊥BD,垂足分别为B、D,求证:AC:EC=BC:DC. 如图,已知在四边形ABED中,点C是线段AB的中点,且∠A=∠B=∠DCE,BE=2,AD=8,那么AC=4.
如图,已知在四边形ABED中,点C是线段AB的中点,且∠A=∠B=∠DCE,BE=2,AD=8,那么AC=4.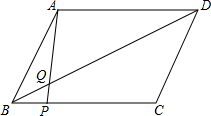 如图,已知?ABCD,BP:PC=1:3,S△BPQ=2cm 2.求:
如图,已知?ABCD,BP:PC=1:3,S△BPQ=2cm 2.求: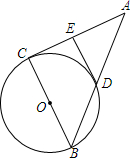 △ABC中,以BC为直径的圆O过边AB的中点D,DE⊥AC,求证:DE为⊙O的切线.
△ABC中,以BC为直径的圆O过边AB的中点D,DE⊥AC,求证:DE为⊙O的切线. 如图,直线l1∥l2,则S△ABC=S△ABD.
如图,直线l1∥l2,则S△ABC=S△ABD.