题目内容
7. 如图,已知在四边形ABED中,点C是线段AB的中点,且∠A=∠B=∠DCE,BE=2,AD=8,那么AC=4.
如图,已知在四边形ABED中,点C是线段AB的中点,且∠A=∠B=∠DCE,BE=2,AD=8,那么AC=4.
分析 由∠A=∠B=∠DCE,根据三角形的内角和和平角的定义得到∠ADC=180°-∠A-∠ACD,∠BCE=180°-∠DCE-∠ACD,求得∠ADC=∠BCE,推出△ACD∽△BCE,根据相似三角形的性质即可得到结论.
解答 解:∵∠A=∠B=∠DCE,
∵∠ADC=180°-∠A-∠ACD,∠BCE=180°-∠DCE-∠ACD,
∴∠ADC=∠BCE,
∴△ACD∽△BCE,
∴$\frac{AD}{BC}$=$\frac{AC}{BE}$,
∵点C是线段AB的中点,
∴AC=BC,
∴AC2=AD•BE=16,
∴AC=4,
故答案为:4.
点评 本题考查了相似三角形的判定和性质,线段的中点,等量代换,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
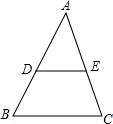 如图,△ABC,DE∥BC,若S△ADE:S梯形DBCE=9:16,那么AD:DB=3:2.
如图,△ABC,DE∥BC,若S△ADE:S梯形DBCE=9:16,那么AD:DB=3:2.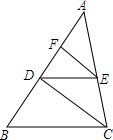 如图,在△ABC中,EF∥DC,DE∥BC,求证:
如图,在△ABC中,EF∥DC,DE∥BC,求证: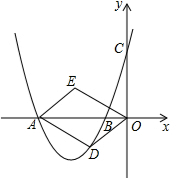 如图,抛物线y=$\frac{3}{4}$x2+$\frac{15}{4}$x+3与x轴交于A、B两点,点D为第三象限的抛物线上一动点.若四边形ODAE是以OA为对角线的平行四边形,且S?ODAE=6,请判断?ODAE是否为菱形?并说明理由.
如图,抛物线y=$\frac{3}{4}$x2+$\frac{15}{4}$x+3与x轴交于A、B两点,点D为第三象限的抛物线上一动点.若四边形ODAE是以OA为对角线的平行四边形,且S?ODAE=6,请判断?ODAE是否为菱形?并说明理由.