题目内容
17.用判别式判别下列方程根的情况(不要求解方程):(1)-x2-3x+1=0;
(2)2x2-$\frac{7}{2}x$+$\frac{1}{4}$=0;
(3)4x2+5=4$\sqrt{5}$x;
(4)$\frac{2}{3}$x2-$\frac{3}{2}x$+$\frac{7}{6}$=0.
分析 (1)根据方程的系数结合根的判别式即可得出△=13>0,由此即可得出方程有两个不相等的实数根;
(2)根据方程的系数结合根的判别式即可得出△=$\frac{41}{4}$>0,由此即可得出方程有两个不相等的实数根;
(3)根据方程的系数结合根的判别式即可得出△=0,由此即可得出方程有两个相等的实数根;
(4)根据方程的系数结合根的判别式即可得出△=-$\frac{31}{36}$<0,由此即可得出方程没有实数根.
解答 解:(1)在方程-x2-3x+1=0中,△=(-3)2-4×(-1)×1=13>0,
∴方程-x2-3x+1=0有两个不相等的实数根;
(2)在方程2x2-$\frac{7}{2}x$+$\frac{1}{4}$=0中,△=$(-\frac{7}{2})^{2}$-4×2×$\frac{1}{4}$=$\frac{41}{4}$>0,
∴方程2x2-$\frac{7}{2}x$+$\frac{1}{4}$=0有两个不相等的实数根;
(3)方程可变形为4x2-4$\sqrt{5}$x+5=0,
在方程4x2+5=4$\sqrt{5}$x中,△=$(-4\sqrt{5})^{2}$-4×4×5=0,
∴方程4x2+5=4$\sqrt{5}$x有两个相等的实数根;
(4)在方程$\frac{2}{3}$x2-$\frac{3}{2}x$+$\frac{7}{6}$=0中,△=$(-\frac{3}{2})^{2}$-4×$\frac{2}{3}$×$\frac{7}{6}$=-$\frac{31}{36}$<0,
∴方程$\frac{2}{3}$x2-$\frac{3}{2}x$+$\frac{7}{6}$=0没有实数根.
点评 本题考查了根的判别式,熟练掌握“当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根”是解题的关键.

| A. | 22017-1 | B. | 22017+1 | C. | 22016-1 | D. | 22016+1 |
①等腰三角形顶角的平分线垂直平分底边;②三角形一个内角的平分线平分这个角的对边,则这个三角形是等腰三角形;③直角三角形直角边上的垂直平分线必过斜边上的中点;④等腰三角形两底角相等.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
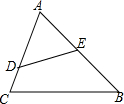 如图,△ABC中,E为AB中点,AB=6,AC=4.5,∠ADE=∠B,则CD=( )
如图,△ABC中,E为AB中点,AB=6,AC=4.5,∠ADE=∠B,则CD=( )| A. | $\frac{3}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |

| A. | 车从济南开往兴化 | B. | 座位号是8 | ||
| C. | 乘车时间是2016年9月28日 | D. | 票价是192元 |
 如图,在正方形ABCD中,AB=4,E是BC边的中点,F是CD边上的一点,且DF=1,若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为$\frac{9\sqrt{5}}{5}$.
如图,在正方形ABCD中,AB=4,E是BC边的中点,F是CD边上的一点,且DF=1,若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为$\frac{9\sqrt{5}}{5}$.