题目内容
5.已知a=$\frac{\sqrt{5}-1}{\sqrt{5}+1}$,则a4-5a3+10a2-11a+4的值为1.分析 由a的值可求出$\frac{1}{a}$的值,将a和$\frac{1}{a}$相加再乘a即可得出a2-3a+1=0,利用分组法分解因式将原式分解成(a2-3a+1)(a2-2a+3)+1,代入a2-3a+1=0即可得出结论.
解答 解:∵a=$\frac{\sqrt{5}-1}{\sqrt{5}+1}$,
∴$\frac{1}{a}$=$\frac{\sqrt{5}+1}{\sqrt{5}-1}$,
∴a+$\frac{1}{a}$=$\frac{\sqrt{5}-1}{\sqrt{5}+1}$+$\frac{\sqrt{5}+1}{\sqrt{5}-1}$=$\frac{(\sqrt{5}-1)^{2}+(\sqrt{5}+1)^{2}}{(\sqrt{5}+1)(\sqrt{5}-1)}$=$\frac{5+1-2\sqrt{5}+5+1+2\sqrt{5}}{5-1}$=$\frac{12}{4}$=3,
两边同时乘a,则:a2+1=3a,
即a2-3a+1=0.
原式=a4-3a3+a2-2a3+6a2+3a2-2a-9a+3+1,
=(a4-3a3+a2)+(-2a3+6a2-2a)+(3a2-9a+3)+1,
=a2(a2-3a+1)-2a(a2-3a+1)+3(a2-3a+1)+1,
=(a2-3a+1)(a2-2a+3)+1,
∵a2-3a+1=0,
∴原式=(a2-3a+1)(a2-2a+3)+1=0+1=1.
故答案为:1.
点评 本题考查了二次根式的化简求值,根据a的值找出a2-3a+1=0是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.若$\frac{a}{b}$=$\frac{1}{2}$,则$\frac{a}{a+b}$的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
16.代数式5x+9与代数式-x+3的值互为相反数,则x的值为( )
| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
13.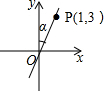 如图,在平面直角坐标系中,直线OP过点(1,3),则tanα的值是( )
如图,在平面直角坐标系中,直线OP过点(1,3),则tanα的值是( )
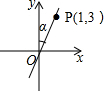 如图,在平面直角坐标系中,直线OP过点(1,3),则tanα的值是( )
如图,在平面直角坐标系中,直线OP过点(1,3),则tanα的值是( )| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
16.某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了15条航线,则这个航空公司共有飞机场( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
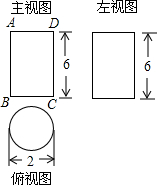 一个几何体的三视图如图所示,如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到CD的中点E,请你求出这个线路的最短路径.
一个几何体的三视图如图所示,如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到CD的中点E,请你求出这个线路的最短路径.