题目内容
 如图,某校数学学习兴趣小组为测量学校旗杆AB的高度,测得教学楼一楼底部C处与旗杆底部B处的水平距离为5米,旗杆底部与教学楼一楼在同一水平线上,在教学楼三楼底部D处测得旗杆顶部A的仰角为27°.若CD的高度为6米,请你帮助该小组计算旗杆AB的高(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.51)
如图,某校数学学习兴趣小组为测量学校旗杆AB的高度,测得教学楼一楼底部C处与旗杆底部B处的水平距离为5米,旗杆底部与教学楼一楼在同一水平线上,在教学楼三楼底部D处测得旗杆顶部A的仰角为27°.若CD的高度为6米,请你帮助该小组计算旗杆AB的高(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.51)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过点D作DE⊥AB于点E,在直角△ADE中,利用三角函数求得AE的长,然后根据AB=AE+BE即可求解.
解答: 解:如图:过点D作DE⊥AB于点E.
解:如图:过点D作DE⊥AB于点E.
由题知,BC=DE=5,BE=DC=6,∠ADE=27°.
在直角△ADE中,tan27°=
.
∴AE=DE•tan27°=5×0.51=2.55(米),
∴AB=AE+BE=6+2.55=8.55≈8.6(米).
答:旗杆AB的高度约为8.6米.
 解:如图:过点D作DE⊥AB于点E.
解:如图:过点D作DE⊥AB于点E. 由题知,BC=DE=5,BE=DC=6,∠ADE=27°.
在直角△ADE中,tan27°=
| AE |
| DE |
∴AE=DE•tan27°=5×0.51=2.55(米),
∴AB=AE+BE=6+2.55=8.55≈8.6(米).
答:旗杆AB的高度约为8.6米.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
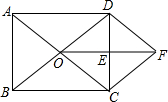 已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证: 如图,
如图,
 已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.