题目内容
 如图,
如图,(1)在梯形ABCD中,AB∥DC,若∠A=∠B,求证:AD=BC.
(2)写出(1)的逆命题,并证明.
考点:梯形,平行四边形的判定与性质,命题与定理
专题:
分析:(1)根据平行线的性质得出四边形ADCE为平行四边形,得出AD=CE,∠CEB=∠A,已知∠A=∠B,得出∠CEB=∠B,从而得出BC=CE,可推出答案.
(2)根据平行线的性质得出四边形ADCE为平行四边形,得出AD=CE,∠CEA=∠A,已知AD=BC,得出CE=BC,从而得出∠CEB=∠B,可推出答案.
(2)根据平行线的性质得出四边形ADCE为平行四边形,得出AD=CE,∠CEA=∠A,已知AD=BC,得出CE=BC,从而得出∠CEB=∠B,可推出答案.
解答: 解:(1)过C作CE∥DA交AB于E,
解:(1)过C作CE∥DA交AB于E,
∴∠A=∠CEB,
又∵∠A=∠B,
∴∠CEB=∠B,
∴BC=EC,
又∵AB∥DC CE∥DA,
∴四边形AECD是平行四边形,
∴AD=EC,
∴AD=BC;
(2)(1)的逆命题:在梯形ABCD中,AB∥DC,若AD=BC,求证:∠A=∠B
证明:过C作CE∥DA交AB于E.
∴∠A=∠CEB,
又∵AB∥DC,CE∥DA,
∴四边形AECD是平行四边形,
∴AD=EC,
又∵AD=BC,
∴BC=EC,
∴∠CEB=∠B,
∴∠A=∠B.
 解:(1)过C作CE∥DA交AB于E,
解:(1)过C作CE∥DA交AB于E,∴∠A=∠CEB,
又∵∠A=∠B,
∴∠CEB=∠B,
∴BC=EC,
又∵AB∥DC CE∥DA,
∴四边形AECD是平行四边形,
∴AD=EC,
∴AD=BC;
(2)(1)的逆命题:在梯形ABCD中,AB∥DC,若AD=BC,求证:∠A=∠B
证明:过C作CE∥DA交AB于E.
∴∠A=∠CEB,
又∵AB∥DC,CE∥DA,
∴四边形AECD是平行四边形,
∴AD=EC,
又∵AD=BC,
∴BC=EC,
∴∠CEB=∠B,
∴∠A=∠B.
点评:本题主要考查对等腰三角形的性质和判定,平行四边形的判定和性质,等腰梯形的判定等知识点的理解和掌握,注意准确作出辅助线是解此题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
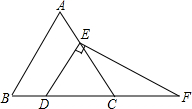 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.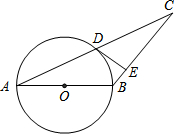 如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DE⊥BC于点E.
如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DE⊥BC于点E. 如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD为多少米?(结果精确到0.1米) (参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD为多少米?(结果精确到0.1米) (参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43) 如图,某校数学学习兴趣小组为测量学校旗杆AB的高度,测得教学楼一楼底部C处与旗杆底部B处的水平距离为5米,旗杆底部与教学楼一楼在同一水平线上,在教学楼三楼底部D处测得旗杆顶部A的仰角为27°.若CD的高度为6米,请你帮助该小组计算旗杆AB的高(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.51)
如图,某校数学学习兴趣小组为测量学校旗杆AB的高度,测得教学楼一楼底部C处与旗杆底部B处的水平距离为5米,旗杆底部与教学楼一楼在同一水平线上,在教学楼三楼底部D处测得旗杆顶部A的仰角为27°.若CD的高度为6米,请你帮助该小组计算旗杆AB的高(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.51)