题目内容
5.有一个内角等于120°的菱形周长为8cm,则较短的对角线长为2cm.较长的对角线与边的夹角是30°,面积是2$\sqrt{3}$cm2.分析 先求出菱形边长,再证明△ABD是等边三角形,得出较短对角线=边长,较长的对角线与边的夹角∠BAC=30°,由勾股定理求出OA,得出AC,关键菱形的面积═$\frac{1}{2}$AC•BD,即可得出结果.
解答 解:如图所示: ∵四边形ABCD是菱形,周长为8cm,∠ABC=120°,
∵四边形ABCD是菱形,周长为8cm,∠ABC=120°,
∴AB=AD=2cm,∠ABC=60°,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC⊥BD,
∴△ABD是等边三角形,
∴BD=AB=2cm,∠BAD=60°,OB=1cm,
∴∠BAC=30°,OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴AC=2$\sqrt{3}$,
∴菱形ABCD的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$;
故答案为:2;30°;2$\sqrt{3}$.
点评 本题考查了菱形的性质、等边三角形的判定、勾股定理以及菱形面积的计算;熟练掌握菱形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
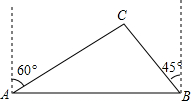 去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2.732km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向、B地的西偏北45°方向C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?($\sqrt{3}$≈1.732)
去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2.732km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向、B地的西偏北45°方向C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?($\sqrt{3}$≈1.732)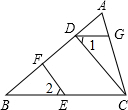 如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.