题目内容
3. 如图,在Rt△ABC中,∠B=90°,D、E分别是AB,AC的中点,且DE=$\sqrt{2}$,梯形BCED的面积为3$\sqrt{6}$,求AB,AC的长.
如图,在Rt△ABC中,∠B=90°,D、E分别是AB,AC的中点,且DE=$\sqrt{2}$,梯形BCED的面积为3$\sqrt{6}$,求AB,AC的长.
分析 先证明DE是△ABC的中位线,由三角形中位线定理得出DE∥BC,BC=2DE=2$\sqrt{2}$,由平行线得出△ADE∽△ABC,得出面积比等于相似比的平方$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=$\frac{1}{4}$,得出△ADE的面积=$\frac{1}{3}$梯形BCED的面积=$\sqrt{6}$,因此△ABC的面积=4$\sqrt{6}$,由△ABC的面积=$\frac{1}{2}$BC•AB,求出AB=4$\sqrt{3}$,再由勾股定理求出AC即可.
解答 解:∵D、E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE=2$\sqrt{2}$,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=$\frac{1}{4}$,
∴△ADE的面积=$\frac{1}{4}$△ABC的面积=$\frac{1}{3}$梯形BCED的面积=$\sqrt{6}$,
∴△ABC的面积=4$\sqrt{6}$,
∵∠B=90°,
∴△ABC的面积=$\frac{1}{2}$BC•AB=4$\sqrt{6}$,
即$\frac{1}{2}$×2$\sqrt{2}$•AB=4$\sqrt{6}$,
∴AB=4$\sqrt{3}$,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{(4\sqrt{3})^{2}+(2\sqrt{2})^{2}}$=2$\sqrt{14}$.
点评 本题考查了三角形中位线定理、相似三角形的判定与性质、勾股定理、三角形面积的计算方法等知识;本题综合性强,难度适中.

(2)按照图中的方式继续排列餐桌,完成下表:
| 桌子张数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 可坐人数 |

(3)每增加-张桌子,可多坐4人;
(4)摆n张桌子时可坐4n+2人;
(5)一家餐厅有长方形桌子30张,现在有131个客人要吃饭,那该如何摆拼桌子?
| 数量x(个) | 1 | 2 | 3 | 4 | 5 |
| 售价y(元) | 8+0.2 | 8+0.4 | 8+0.6 | 8+0.8 | 8+1.0 |

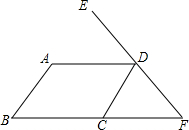 如图,AB∥CD,AD∥BC,∠B=60°,∠EDA=50°,求∠CDF.
如图,AB∥CD,AD∥BC,∠B=60°,∠EDA=50°,求∠CDF.