题目内容
6.方程2x2-6x+3=0的根的情况是( )| A. | 有两个同号的不相等的实数根 | B. | 有两个异号的不相等的实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
分析 计算出△=b2-4ac的值即可判断根的个数,再根据韦达定理可得两根之积大于0,即两根同号.
解答 解:∵a=2,b=-6,c=3,
∴△=b2-4ac=(-6)2-4×2×3=12>0,x1x2=$\frac{3}{2}$>0,
∴方程有两个同号不相等的实数根,
故选:A.
点评 本题主要考查利用一元二次方程根的判别式(△=b2-4ac)判断方程的根的情况及韦达定理得应用.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.

练习册系列答案
相关题目
16.下列关于x的方程中,没有实数解的是( )
| A. | x2-4x+4=0 | B. | x2-2x-3=0 | C. | x2-2x=0 | D. | x2-2x+5=0 |
17. 如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF:CF=( )
如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF:CF=( )
 如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF:CF=( )
如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF:CF=( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 2:5 |
14.下列计算正确的是( )
| A. | -2(x+3y)=-2x+3y | B. | -2(x+3y)=-2x-3y | C. | -2(x+3y)=-2x+6y | D. | -2(x+3y)=-2x-6y |
11.关于x的一元二次方程|m|x2-2x+1=0有两个不相等的实数根,则m的取值范围是( )
| A. | -1<m<1 | B. | -1<m<1且m≠0 | C. | m>1 | D. | m<1且m≠0 |
18.同一平面内,半径分别是2cm和3cm的两圆的圆心距为5cm,则这两圆的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
15.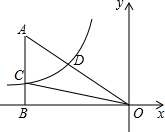 如图,已知双曲线y=-$\frac{3}{x}$(x<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,则△AOC的面积为( )
如图,已知双曲线y=-$\frac{3}{x}$(x<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,则△AOC的面积为( )
 如图,已知双曲线y=-$\frac{3}{x}$(x<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,则△AOC的面积为( )
如图,已知双曲线y=-$\frac{3}{x}$(x<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,则△AOC的面积为( )| A. | 6 | B. | $\frac{9}{2}$ | C. | 3 | D. | 2 |