题目内容
19.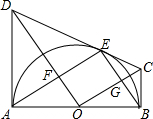 如图,已知AB为⊙O的直径,AD、BC、CD为⊙O的切线,切点分别是A、B、E,则有以下结论:(1)CO⊥DO;(2)四边形OFEG是矩形,试说明理由.
如图,已知AB为⊙O的直径,AD、BC、CD为⊙O的切线,切点分别是A、B、E,则有以下结论:(1)CO⊥DO;(2)四边形OFEG是矩形,试说明理由.
分析 (1)根据切线长定理得到OD平分∠ADE,OC平分∠BCE,根据切线的性质得AD⊥AB,BC⊥AB,则∠ODC=$\frac{1}{2}$(∠ADC+∠BCD),再利用AD∥BC得到∠ADC+BCD=180°,所以∠ODC+∠OCD=90°,于是可判断CO⊥DO;
(2)根据切线长定理得DA=DE,CE=CB,而OD平分∠ADE,OC平分∠BCE,根据角平分线定理的逆定理得到DF⊥AE,CG⊥BE,∠OFE=90°,∠OGE=90°,加上∠FOG=90°,于是可判断四边形OFEG是矩形.
解答 解:(1)∵AD、BC、CD为⊙O的切线,
∴OD平分∠ADE,OC平分∠BCE,AD⊥AB,BC⊥AB,
∴∠ODC=$\frac{1}{2}$∠ADC,∠OCD=$\frac{1}{2}$∠BCD,
∴∠ODC+∠OCD=$\frac{1}{2}$(∠ADC+∠BCD),
∵AD∥BC,
∴∠ADC+BCD=180°,
∴∠ODC+∠OCD=$\frac{1}{2}$×180°=90°,
∴∠DOC=90°,
∴CO⊥DO;
(2)∵AD、BC、CD为⊙O的切线,
∴DA=DE,CE=CB,
而OD平分∠ADE,OC平分∠BCE,
∴DF⊥AE,CG⊥BE,
∴∠OFE=90°,∠OGE=90°,
而∠FOG=90°,
∴四边形OFEG是矩形.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了切线长定理和矩形的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠OAB等于( )
如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠OAB等于( )
 如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠OAB等于( )
如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MOB和∠OAB等于( )| A. | 50°和30° | B. | 40°和70° | C. | 30°和 20° | D. | 20°和70° |
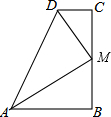 如图,∠B=∠C=90°,AD=AB+CD,DM平分∠ADC,求证:M是BC的中点.
如图,∠B=∠C=90°,AD=AB+CD,DM平分∠ADC,求证:M是BC的中点.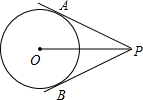 如图,P是⊙O外一点,PA,PB是⊙O的两条切线,A,B为切点,OP交⊙O于点C,PA=4cm,PC=2cm,求∠APB的大小.
如图,P是⊙O外一点,PA,PB是⊙O的两条切线,A,B为切点,OP交⊙O于点C,PA=4cm,PC=2cm,求∠APB的大小.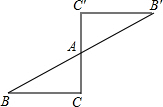 如图,△ABC绕点A旋转180°,得到△A′B′C′,A为旋转中心,则△ABC与△A′B′C′关于点A中心对称;若∠C=90°,∠B=30°,BC=1,则BB′的长为$\frac{4\sqrt{3}}{3}$.
如图,△ABC绕点A旋转180°,得到△A′B′C′,A为旋转中心,则△ABC与△A′B′C′关于点A中心对称;若∠C=90°,∠B=30°,BC=1,则BB′的长为$\frac{4\sqrt{3}}{3}$.