题目内容
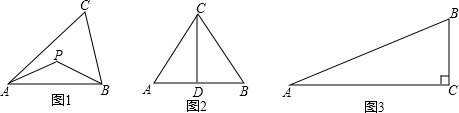
联想三角形外心的概念,我们可引入如下概念:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.例:已知PA=PB,则点P为△ABC的准外心(如图1).
(1)如图2,CD为正三角形ABC的高,准外心P在高CD上,且PD=
AB,求∠APB的度数.
(2)如图3,若△ABC为直角三角形,∠C=90°,AB=13,BC=5,准外心P在AC边上,试探究PA的长.
(1)如图2,CD为正三角形ABC的高,准外心P在高CD上,且PD=
| 1 |
| 2 |
(2)如图3,若△ABC为直角三角形,∠C=90°,AB=13,BC=5,准外心P在AC边上,试探究PA的长.

考点:三角形的外接圆与外心
专题:几何图形问题,新定义
分析:(1)利用分类讨论:①若PB=PC,②若PA=PC,③若PA=PB,进而求出即可;
(2)利用分类讨论:①若PB=PA,②若PA=PC,③若PC=PB,进而求出即可.
(2)利用分类讨论:①若PB=PA,②若PA=PC,③若PC=PB,进而求出即可.
解答: 解:(1)①若PB=PC,连结PB,则∠PCB=∠PBC.
解:(1)①若PB=PC,连结PB,则∠PCB=∠PBC.
∵CD为等边三角形的高.∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,∴PD=
DB=
AB.
与已知PD=
AB矛盾,∴PB≠PC.
②若PA=PC,连结PA,则∠PCA=∠PAC.
∵CD为等边三角形的高.∴AD=BD,∠PCA=30°,
∴∠PAD=∠PAC=30°,∴PD=
DA=
AB.
与已知PD=
AB矛盾,∴PA≠PC.
③若PA=PB,由PD=
AB,得PD=BD,
∴∠BPD=45°,
故∠APB=90°;
(2)①若PB=PA,设PA=x,
∵∠C=90°,AB=13,BC=5,
∴AC=12,则CP=12-x,
∴x2=(12-x)2+52,
∴解得:x=
,即PA=
.
②若PA=PC,则PA=6.
③若PC=PB,由图知,在Rt△PBC中,不可能,
故PA=
或6.
 解:(1)①若PB=PC,连结PB,则∠PCB=∠PBC.
解:(1)①若PB=PC,连结PB,则∠PCB=∠PBC.∵CD为等边三角形的高.∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,∴PD=
| ||
| 3 |
| ||
| 6 |
与已知PD=
| 1 |
| 2 |
②若PA=PC,连结PA,则∠PCA=∠PAC.
∵CD为等边三角形的高.∴AD=BD,∠PCA=30°,
∴∠PAD=∠PAC=30°,∴PD=
| ||
| 3 |
| ||
| 6 |
与已知PD=
| 1 |
| 2 |
③若PA=PB,由PD=
| 1 |
| 2 |
∴∠BPD=45°,
故∠APB=90°;
(2)①若PB=PA,设PA=x,
∵∠C=90°,AB=13,BC=5,
∴AC=12,则CP=12-x,
∴x2=(12-x)2+52,
∴解得:x=
| 169 |
| 24 |
| 169 |
| 24 |
②若PA=PC,则PA=6.
③若PC=PB,由图知,在Rt△PBC中,不可能,
故PA=
| 169 |
| 24 |
点评:此题主要考查了勾股定理以及三角形外心的性质等知识,利用分类讨论得出是解题关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
点P(3,-1)在第( )象限.
| A、一 | B、二 | C、三 | D、四 |
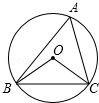 如图,△ABC内接于⊙O,∠BAC=60°,⊙O的半径为2,求BC的长(保留根号).
如图,△ABC内接于⊙O,∠BAC=60°,⊙O的半径为2,求BC的长(保留根号).