题目内容
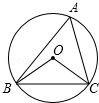如图，△ABC内接于⊙O，∠BAC=60°，⊙O的半径为2，求BC的长（保留根号）．考点：垂径定理,圆周角定理
专题：几何图形问题,数形结合
分析：首先过点O作OD⊥BC于D，由垂径定理可得BC=2BD，又由圆周角定理，可求得∠BOC的度数，然后根据等腰三角形的性质，求得∠OBC的度数，利用余弦函数，即可求得答案．
解答：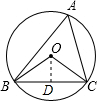
解：过点O作OD⊥BC于D，
则BC=2BD，
∵△ABC内接于⊙O，∠BAC=60°，
∴∠BOC=2∠A=120°，
∵OB=OC，
∴∠OBC=∠OCB=
=30°，
∵⊙O的半径为2，
∴BD=OB•cos∠OBC=2×
=
，
∴BC=2
．
故答案为：2
．
解：过点O作OD⊥BC于D，则BC=2BD，
∵△ABC内接于⊙O，∠BAC=60°，
∴∠BOC=2∠A=120°，
∵OB=OC，
∴∠OBC=∠OCB=
| 180°-∠BOC |
| 2 |
∵⊙O的半径为2，
∴BD=OB•cos∠OBC=2×
| ||
| 2 |
| 3 |
∴BC=2
| 3 |
故答案为：2
| 3 |
点评：此题考查了圆周角定理、垂径定理、等腰三角形的性质以及三角函数等知识．此题难度不大，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
相关题目
下列一元二次方程中，有两个相等的实数根的是（ ）
| A、x2-2x+1=0 |
| B、x2+2x-4=0 |
| C、x2-2x-5=0 |
| D、x2+2x+4=0 |
若样本x1+1，x2+1，x3+1，…，xn+1的平均数为18，方差为2，则对于样本x1+2，x2+2，x3+2，…，xn+2，下列结论正确的是（ ）
| A、平均数为18，方差为2 |
| B、平均数为19，方差为3 |
| C、平均数为19，方差为2 |
| D、平均数为20，方差为4 |
