题目内容
已知抛物线y=x2+bx+c与y轴交于点Q(0,-3),图象与x轴两交点的横坐标的平方和为15,求函数解析式及对称轴.
考点:抛物线与x轴的交点
专题:
分析:根据点Q的坐标易求抛物线的解析式为y=x2+bx-3.然后结合一元二次方程的根与系数的关系列出关于b的方程,通过解方程来求b的值;再由对称轴公式求得对称轴或者将函数式转化为顶点式,然后找对称轴.
解答:解:由点Q(0,-3)知c=-3,则该抛物线的解析式为y=x2+bx-3.
设α、β是关于x的方程x2+bx-3=0的两根,
则α+β=-b,αβ=-3,
∴α2+β2=(α+β)2-2αβ=b2+6=15,
解得 b=±3,
∴所求函数解析式为:y=x2+3x-3或y=x2-3x-3.
∴对称轴分别为:x=-
或x=
.
设α、β是关于x的方程x2+bx-3=0的两根,
则α+β=-b,αβ=-3,
∴α2+β2=(α+β)2-2αβ=b2+6=15,
解得 b=±3,
∴所求函数解析式为:y=x2+3x-3或y=x2-3x-3.
∴对称轴分别为:x=-
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了抛物线与x轴的交点.解题时,注意利用完全平方公式的变形得到关于b的方程并求得b的值.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 已知一次函数y=kx+b与反比例函数y=
已知一次函数y=kx+b与反比例函数y=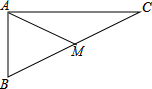 如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.
如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.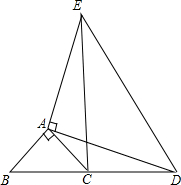 如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.则线段BD与CE有什么关系?请说明理由.
如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.则线段BD与CE有什么关系?请说明理由.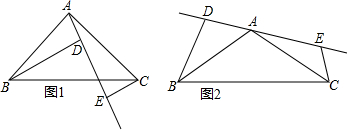
 如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为灰色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为灰色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖. 如图,△ABC中,D、E分别为边AB、AC的中点.证明:△ADE∽△ABC.
如图,△ABC中,D、E分别为边AB、AC的中点.证明:△ADE∽△ABC.