题目内容
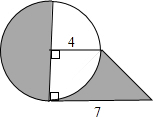 求阴影部分的面积:
求阴影部分的面积:考点:扇形面积的计算
专题:
分析:求得S梯形OABC,S扇形OAC,以及S半圆OCmD,根据S阴影=S梯形OABC+S半圆OCmD-S扇形OAC求解.
解答: 解:S梯形OABC=
解:S梯形OABC=
(OA+BC)•OC=
(4+7)×4=22,
S扇形OAC=
π×42=4π,
S半圆OCmD=
π×42=8π,
则S阴影=S梯形OABC+S半圆OCmD-S扇形OAC=22+8π-4π=22+4π.
 解:S梯形OABC=
解:S梯形OABC=| 1 |
| 2 |
| 1 |
| 2 |
S扇形OAC=
| 1 |
| 4 |
S半圆OCmD=
| 1 |
| 2 |
则S阴影=S梯形OABC+S半圆OCmD-S扇形OAC=22+8π-4π=22+4π.
点评:本题考查了扇形和梯形的面积公式,正确利用规图形的面积表示出不规则图形的面积是关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
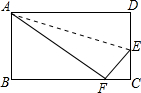 折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )
折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )A、5
| ||
B、5
| ||
| C、12cm | ||
| D、13cm |
 b=b2-a-1,例如:7
b=b2-a-1,例如:7 4=42-7-1=8,那么(-5)
4=42-7-1=8,那么(-5) (-3)=
(-3)= 已知一次函数y=kx+b与反比例函数y=
已知一次函数y=kx+b与反比例函数y=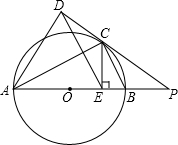 PC切圆O于C,PBA为过圆心O的割线,点D在射线PC上,CE⊥AB于E,AC平分∠DAB,连接DE,CB,求证:DE∥BC.
PC切圆O于C,PBA为过圆心O的割线,点D在射线PC上,CE⊥AB于E,AC平分∠DAB,连接DE,CB,求证:DE∥BC.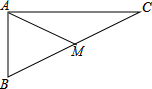 如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线.
如图,在△ABC中,∠ABC=90°,AB=4cm,AC=6cm,AM是中线. 如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.则线段BD与CE有什么关系?请说明理由.
如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.则线段BD与CE有什么关系?请说明理由.