题目内容
11．求出y=-x2+2的对称轴和顶点坐标，并在直角坐标系中画山函数图象．分析 （1）利用配方法求出二次函数的对称轴和顶点坐标即可；
（2）把握抛物线与x轴，y轴的交点，顶点坐标，开口方向等画出图象即可．
解答 
解：y=-x2+2的对称轴是y轴，顶点坐标（0，2），如图所示；
点评 此题主要考查了配方法求二次函数的对称轴和顶点坐标，此题是二次函数的基本性质也是考查重点，同学们应熟练掌握．
练习册系列答案
相关题目
1．
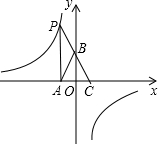如图，点P是反比例函数y=$\frac{k}{x}$（k＜0）图象上的点，PA垂直x轴于点A（-1，0），点C的坐标为（1，0），PC交y轴于点B，连结AB，已知AB=$\sqrt{5}$，则k的值等于（ ）
如图，点P是反比例函数y=$\frac{k}{x}$（k＜0）图象上的点，PA垂直x轴于点A（-1，0），点C的坐标为（1，0），PC交y轴于点B，连结AB，已知AB=$\sqrt{5}$，则k的值等于（ ）| A． | 2 | B． | -2 | C． | -4 | D． | -6 |
2．
如图，矩形ABCD中，E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F．若AB=4，BC=6，则FD的长为 （ ）
如图，矩形ABCD中，E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F．若AB=4，BC=6，则FD的长为 （ ）| A． | $\frac{8}{5}$ | B． | 4 | C． | $\frac{9}{4}$ | D． | $2\sqrt{3}$ |
19．若$\frac{{3\sqrt{x+1}}}{x-2}$有意义，则x应满足的条件是（ ）
| A． | x≠-1 | B． | x≥2 | C． | x≠2 | D． | x≥-1且x≠2 |
6．
如图，将△ABC沿AB方向向右平移得到△DEF，其中AF=8，DB=2，则平移的距离为（ ）
如图，将△ABC沿AB方向向右平移得到△DEF，其中AF=8，DB=2，则平移的距离为（ ）| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
16．下列命题中，真命题是（ ）
| A． | 有两边相等的平行四边形是菱形 | B． | 对角线垂直的四边形是菱形 | ||
| C． | 有一角为90°菱形是正方形 | D． | 对角线相等的四边形是矩形 |
3．
一次函数y=-$\frac{3}{2}$x+3的图象如图所示，当y＞0时x的取值范围是（ ）
一次函数y=-$\frac{3}{2}$x+3的图象如图所示，当y＞0时x的取值范围是（ ）| A． | x＞2 | B． | x＜2 | C． | x＜0 | D． | 2＜x＜4 |
20．在平面内过O点作三条射线OA、OB、OC，已知∠AOB=50°，∠BOC=20°，则∠AOC的度数为（ ）
| A． | 70° | B． | 30° | C． | 70°或30° | D． | 无法确定 |