题目内容
13.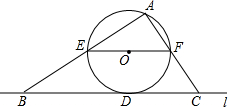 如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为$\frac{7}{5}$.
如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为$\frac{7}{5}$.
分析 连接OD,作EH⊥BC,如图,先利用圆周角定理得到∠A=90°,再利用等角的余角相等得到∠BEH=∠C,接着根据切线的性质得到OD⊥BC,易得四边形EHOD为正方形,则EH=OD=OE=HD=5,所以BH=7,然后根据正切的定义得到tan∠BEH=$\frac{7}{5}$,从而得到tan∠ACB的值.
解答 解:连接OD,作EH⊥BC,如图,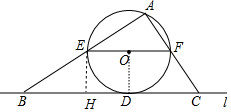
∵EF为直径,
∴∠A=90°,
∵∠B+∠C=90°,∠B+∠BEH=90°,
∴∠BEH=∠C,
∵直线l与⊙相切于点D,
∴OD⊥BC,
而EH⊥BC,EF∥BC,
∴四边形EHOD为正方形,
∴EH=OD=OE=HD=5,
∴BH=BD-HD=7,
在Rt△BEH中,tan∠BEH=$\frac{BH}{EH}$=$\frac{7}{5}$,
∴tan∠ACB=$\frac{7}{5}$.
故答案为$\frac{7}{5}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了正切的定义.

练习册系列答案
相关题目
3. 一次函数y=-$\frac{3}{2}$x+3的图象如图所示,当y>0时x的取值范围是( )
一次函数y=-$\frac{3}{2}$x+3的图象如图所示,当y>0时x的取值范围是( )
 一次函数y=-$\frac{3}{2}$x+3的图象如图所示,当y>0时x的取值范围是( )
一次函数y=-$\frac{3}{2}$x+3的图象如图所示,当y>0时x的取值范围是( )| A. | x>2 | B. | x<2 | C. | x<0 | D. | 2<x<4 |
8. 如图,AB是⊙O的直径,DC是弦,若∠COB=68°,则∠BDC的度数等于( )
如图,AB是⊙O的直径,DC是弦,若∠COB=68°,则∠BDC的度数等于( )
 如图,AB是⊙O的直径,DC是弦,若∠COB=68°,则∠BDC的度数等于( )
如图,AB是⊙O的直径,DC是弦,若∠COB=68°,则∠BDC的度数等于( )| A. | 30° | B. | 32° | C. | 34° | D. | 45° |
18. 若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
 若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )
若函数y=kx-b的图象如图所示,则关于x的不等式k(x-3)-b>0的解集为( )| A. | x<3 | B. | x>2 | C. | x<5 | D. | x>5 |
 我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.
我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.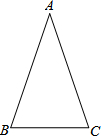 如图,在△ABC中,AB=AC,∠A=36°,且BC=2,则AB=$\sqrt{5}+1$.
如图,在△ABC中,AB=AC,∠A=36°,且BC=2,则AB=$\sqrt{5}+1$.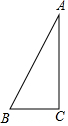 △ABC中,∠C=90°,∠B=60°,AC=3,以C为圆心,r为半径作⊙C,如果点B在圆内,而点A在圆外,那么r的取值范围是$\sqrt{3}$<r<3.
△ABC中,∠C=90°,∠B=60°,AC=3,以C为圆心,r为半径作⊙C,如果点B在圆内,而点A在圆外,那么r的取值范围是$\sqrt{3}$<r<3.