题目内容
如图1,在平面直角坐标系中,O是坐标原点,长方形ABCD的顶点C(3,
),顶点A在x轴的负半轴上,顶点B在x轴上.点E是CD上一动点,将梯形OBCE沿OE翻折至OB′C′E,OB′交CD于H,过点O作OE的垂线交CD所在直线于点G,设E(t,
).
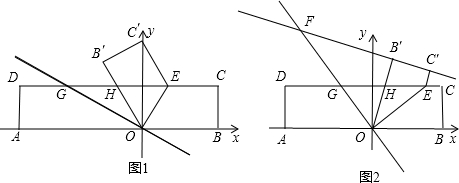
(1)直接写出OB′的长;
(2)①当HB′=1时,求出对应H点的坐标;②求证:HG=HO.
(3)如图2,作直线B′C′交直线OG于F.在运动变化过程中,点F的横坐标会随着t的变化而变化吗?如果变化,请用含t的式子表示;如果不变,求出点F的横坐标.
| 3 |
| 3 |

(1)直接写出OB′的长;
(2)①当HB′=1时,求出对应H点的坐标;②求证:HG=HO.
(3)如图2,作直线B′C′交直线OG于F.在运动变化过程中,点F的横坐标会随着t的变化而变化吗?如果变化,请用含t的式子表示;如果不变,求出点F的横坐标.
考点:四边形综合题
专题:综合题
分析:(1)由C的坐标确定出OB的长,利用折叠性质即可确定出OB′的长;
(2)①当HB′=1时,得到OH=2,设CD与y轴的交点为M,分两种情况考虑:(i)当H在y轴左侧时,利用勾股定理求出MH的长,确定出H坐标;(ii)当H在y轴右侧时,同理得出MH,确定出此时H坐标;
②由折叠的性质得到一对角相等,再由CD与AB平行得到一对内错角相等,等量代换及等角对等边得到EH=HO,由OE垂直于OG,得到两对角互余,利用等角的余角相等得到∠GOH=∠HGO,利用等角对等边得到HG=HO,等量代换得到HG=HE;
(3)在运动变化过程中,点F的横坐标不变,理由为:过F作FN⊥AB于N,由CD与AB平行得到一对内错角相等,由∠GOH=∠HGO,等量代换得到一对角相等,再由一对直角相等,OF=OF,利用AAS得到△FON≌△FB′O,利用全等三角形对应边相等得到ON=OB′=3,即F横坐标不变为3.
(2)①当HB′=1时,得到OH=2,设CD与y轴的交点为M,分两种情况考虑:(i)当H在y轴左侧时,利用勾股定理求出MH的长,确定出H坐标;(ii)当H在y轴右侧时,同理得出MH,确定出此时H坐标;
②由折叠的性质得到一对角相等,再由CD与AB平行得到一对内错角相等,等量代换及等角对等边得到EH=HO,由OE垂直于OG,得到两对角互余,利用等角的余角相等得到∠GOH=∠HGO,利用等角对等边得到HG=HO,等量代换得到HG=HE;
(3)在运动变化过程中,点F的横坐标不变,理由为:过F作FN⊥AB于N,由CD与AB平行得到一对内错角相等,由∠GOH=∠HGO,等量代换得到一对角相等,再由一对直角相等,OF=OF,利用AAS得到△FON≌△FB′O,利用全等三角形对应边相等得到ON=OB′=3,即F横坐标不变为3.
解答:解:(1)∵C(3,
),
∴OB=3,
由折叠可得OB′=OB=3;
(2)①当HB′=1时,OH=2,
设CD与y轴的交点为M,

分两种情况考虑:
(i)当H在y轴左侧时,利用勾股定理得:MH=1,
此时H(-1,
);
(ii)当H在y轴右侧时,同理MH=1,
此时H(1,
),
综上,H(-1,
)或(1,
);
②由折叠可得∠BOE=∠HOE,
∵CD∥AB,
∴∠BOE=∠HEO,
∴∠HEO=∠HOE,
∴HE=HO,
∵∠EOG=90°,
∴∠GOH+∠HOE=90°,∠OGE+∠HEO=90°,
∵∠HOE=∠HEO,
∴∠GOH=∠HGO,
∴HG=HO,
∵HE=HO,
∴HG=HE;
(3)在运动变化过程中,点F的横坐标不变,理由为:
过F作FN⊥AB于N,

∵CD∥AB,
∴∠HGO=∠GOA,
∵∠GOH=∠HGO,
∴∠GOA=∠GOH,
在△FON和△FB′O中,
,
∴△FON≌△FB′O(AAS),
∴ON=OB′=3,
则点F的横坐标保持不变,它的横坐标为-3.
| 3 |
∴OB=3,
由折叠可得OB′=OB=3;
(2)①当HB′=1时,OH=2,
设CD与y轴的交点为M,

分两种情况考虑:
(i)当H在y轴左侧时,利用勾股定理得:MH=1,
此时H(-1,
| 3 |
(ii)当H在y轴右侧时,同理MH=1,
此时H(1,
| 3 |
综上,H(-1,
| 3 |
| 3 |
②由折叠可得∠BOE=∠HOE,
∵CD∥AB,
∴∠BOE=∠HEO,
∴∠HEO=∠HOE,
∴HE=HO,
∵∠EOG=90°,
∴∠GOH+∠HOE=90°,∠OGE+∠HEO=90°,
∵∠HOE=∠HEO,
∴∠GOH=∠HGO,
∴HG=HO,
∵HE=HO,
∴HG=HE;
(3)在运动变化过程中,点F的横坐标不变,理由为:
过F作FN⊥AB于N,

∵CD∥AB,
∴∠HGO=∠GOA,
∵∠GOH=∠HGO,
∴∠GOA=∠GOH,
在△FON和△FB′O中,
|
∴△FON≌△FB′O(AAS),
∴ON=OB′=3,
则点F的横坐标保持不变,它的横坐标为-3.
点评:此题属于四边形综合题,涉及的知识有:全等三角形的判定与性质,坐标与图形性质,平行线的性质,等腰三角形的判定与性质,以及勾股定理,熟练掌握判定与性质是解本题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
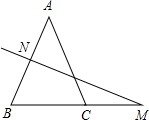 已知:如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.
已知:如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°. 如图,?ABCD的对角线AC的垂直平分线与AD,BC分别交于点E,F.
如图,?ABCD的对角线AC的垂直平分线与AD,BC分别交于点E,F. △ABC在方格中,位置如图,A点的坐标为(-3,1).
△ABC在方格中,位置如图,A点的坐标为(-3,1).