题目内容
 如图,点E是?ABCD中的边BC上的一点,AE交BD于点F,BE=3,BC=4,S△FBE=18,求?ABCD的面积.
如图,点E是?ABCD中的边BC上的一点,AE交BD于点F,BE=3,BC=4,S△FBE=18,求?ABCD的面积.考点:平行四边形的性质
专题:
分析:由条件可得BF:FD=BE:BC=3:4,可求得△AFD的面积和△ABF的面积,再由△ABD≌△CDB,可求得四边形ABCD的面积.
解答:解:
∵四边形ABCD为平行四边形,
∴BC=AD=4,AD∥BC
∴
=
=
=
,且△BEF∽△DAF,
∴
=(
)2=
,
即
=
,
∴S△ADF=32,
又∵△ABF和△ADF同高,
∴
=
=
,
即
=
,
∴S△ABF=24,
∴S△ABD=24+32=56,
在△ABD和△CDB中
∴△ABD≌△CDB(SSS),
∴S△ABD=S△CDB,
∴S四边形ABCD=2S△ABD=112.
∵四边形ABCD为平行四边形,
∴BC=AD=4,AD∥BC
∴
| BF |
| DF |
| BE |
| AD |
| BE |
| BC |
| 3 |
| 4 |
∴
| S△BEF |
| S△ADF |
| 3 |
| 4 |
| 9 |
| 16 |
即
| 18 |
| S△ADF |
| 9 |
| 16 |
∴S△ADF=32,
又∵△ABF和△ADF同高,
∴
| S△ABF |
| S△ADF |
| BF |
| DF |
| 3 |
| 4 |
即
| S△ABF |
| 32 |
| 3 |
| 4 |
∴S△ABF=24,
∴S△ABD=24+32=56,
在△ABD和△CDB中
|
∴△ABD≌△CDB(SSS),
∴S△ABD=S△CDB,
∴S四边形ABCD=2S△ABD=112.
点评:本题主要考查平行四边形的性质及相似三角形的判定和性质,由条件求得△ADF和△ABF的面积是解题的关键,注意利用等高同底或等底同高的两个三角形面积的关系.

练习册系列答案
相关题目
桌上摆满了朋友们送来的礼物,小狗贝贝好奇地想看个究竟.①小狗先是站在地面上看,②然后抬起了前腿看,③唉,还是站到凳子上看吧,④最后,它终于爬上了桌子…请你根据小狗四次看礼物的顺序,把图乙四副图片按对应字母正确排序为( )
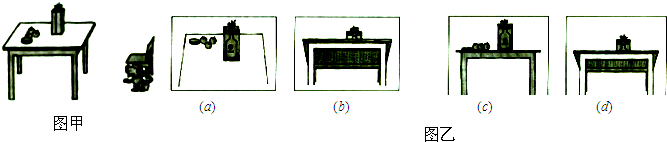

| A、(a) (b) (c) (d) |
| B、(c) (b) (d) (a) |
| C、(b) (a) (c) (d) |
| D、(b) (d) (c) (a) |
下列说法正确的是( )
| A、最小的整数是1 |
| B、最大的负数是-1 |
| C、最大的负整数是-1 |
| D、最小的有理数是0 |
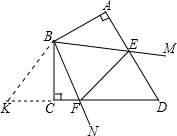 已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=
已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=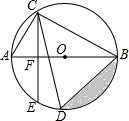 已知AB是⊙O的直径,AB=10cm,弦AC=6cm,弦CE⊥AB,垂足为F,弦CD平分∠ACB.
已知AB是⊙O的直径,AB=10cm,弦AC=6cm,弦CE⊥AB,垂足为F,弦CD平分∠ACB. 如图,将矩形ABCD折叠,使点D与B重合,点C落在点C′外,折痕为EF,如果∠ABE=20°,则∠EFC′=
如图,将矩形ABCD折叠,使点D与B重合,点C落在点C′外,折痕为EF,如果∠ABE=20°,则∠EFC′= 如图,已知NG平分∠BNF,∠AMD=∠MNF,∠CMN:∠DMN=3:5,试求∠MNF和∠GNF的度数.
如图,已知NG平分∠BNF,∠AMD=∠MNF,∠CMN:∠DMN=3:5,试求∠MNF和∠GNF的度数. 如图,在△ABC中,AC=AB,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,求△BCF的周长和∠EFC的度数.
如图,在△ABC中,AC=AB,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,求△BCF的周长和∠EFC的度数.