题目内容
10.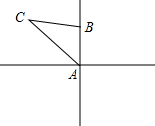 如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )
如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )| A. | 40海里 | B. | 30海里 | C. | 20海里 | D. | 10海里 |
分析 根据题意得出∠CAB=30°,∠CBF=60°,进而得出△ABC是等腰三角形,求出BC的长即可.
解答  解:过点C作CF⊥AB于点F,
解:过点C作CF⊥AB于点F,
由题意可得:AB=20海里,∠CAB=30°,∠CBF=60°,
故∠ACB=30°,即∠CAB=∠ACB,则BC=AB=20海里.
故选:C.
点评 此题主要考查了解直角三角形的应用,根据题意得出△ABC是等腰三角形是解题关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
5.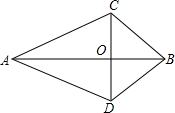 如图,AC=AD,BC=BD,则下列结果正确的是( )
如图,AC=AD,BC=BD,则下列结果正确的是( )
 如图,AC=AD,BC=BD,则下列结果正确的是( )
如图,AC=AD,BC=BD,则下列结果正确的是( )| A. | ∠ABC=∠CAB | B. | OA=OB | C. | ∠ACD=∠BDC | D. | AB⊥CD |
 如图所示的半圆中,AD是直径,且AD=3,AC=2,则sin∠ABC的值是$\frac{2}{3}$.
如图所示的半圆中,AD是直径,且AD=3,AC=2,则sin∠ABC的值是$\frac{2}{3}$.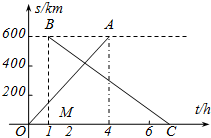 甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题:
甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题:



 两个边长分别为2cm和3cm的正方形如图摆放,则图中阴影部分的面积为$\frac{7}{2}$cm2.
两个边长分别为2cm和3cm的正方形如图摆放,则图中阴影部分的面积为$\frac{7}{2}$cm2.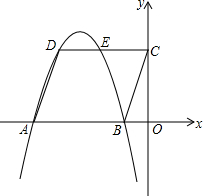 已知:平行四边形ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S□ABCD=12,抛物线经过D、A、B三点.
已知:平行四边形ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S□ABCD=12,抛物线经过D、A、B三点.