题目内容
19.已知:关于的方程x2-(k+1)x+$\frac{1}{4}$k2+1=0的两根是一个矩形两邻边的长.(1)求k实数的取值范围;
(2)当矩形的对角线长为$\sqrt{5}$时,求实数k的值.
分析 (1)根据一元二次方程根的判别式,方程有两个实数根,则判别式△≥0,得出关于k的不等式,求出k的取值范围.
(2)根据勾股定理和根与系数的关系得出关于k的方程,求出k的值并检验.
解答 解:(1)设方程的两根为x1,x2
则△=[-(k+1)]2-4($\frac{1}{4}$k2+1)=2k-3,
∵方程有两个实数根,∴△≥0,
即2k-3≥0,
∴k≥$\frac{3}{2}$.
(2)由题意得:$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=k+1}\\{{x}_{1}{x}_{2}=\frac{1}{4}{k}^{2}+1}\end{array}\right.$,
又∵x12+x22=5,即(x1+x2)2-2x1x2=5,
(k+1)2-2($\frac{1}{4}$k2+1)=5,
整理得k2+4k-12=0,
解得k=2或k=-6(舍去),
∴k的值为2.
点评 此题考查一元二次方程的实际运用,解决本题的关键是利用一元二次方程根与系数的关系和勾股定理,把问题转化为解方程求得k的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.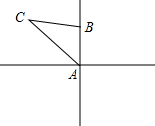 如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )
如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )
 如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )
如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )| A. | 40海里 | B. | 30海里 | C. | 20海里 | D. | 10海里 |
14. 有理数a、b、c在数轴上的位置如图,则下列关系正确的是( )
有理数a、b、c在数轴上的位置如图,则下列关系正确的是( )
 有理数a、b、c在数轴上的位置如图,则下列关系正确的是( )
有理数a、b、c在数轴上的位置如图,则下列关系正确的是( )| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>a>b |
4.如图(一),在边长为a的正方形中,挖掉一个边长为b的小正方形(a>b),把余下的部分剪成一个矩形(如图(二)),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
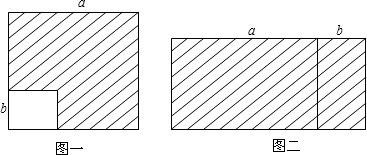

| A. | (a+b)2=a2+2ab+b2 | B. | a2-b2=(a+b)(a-b) | ||
| C. | (a-b)2=a2-2ab+b2 | D. | (a+2b)(a-b)=a2+ab-2b2 |
 解不等式组3x-1<2(x+1)并把解集在数轴上表示出来.
解不等式组3x-1<2(x+1)并把解集在数轴上表示出来.