题目内容
1. 如图所示的半圆中,AD是直径,且AD=3,AC=2,则sin∠ABC的值是$\frac{2}{3}$.
如图所示的半圆中,AD是直径,且AD=3,AC=2,则sin∠ABC的值是$\frac{2}{3}$.
分析 根据圆周角定理得出∠ACB=90°,∠ABC=∠ADC,解直角三角形求出即可.
解答 解:∵∠ABC和∠ADC都对$\widehat{AC}$,
∴∠ABC=∠ADC,
∵AD是直径,
∴∠ACD=90°,
∴sin∠ABC=sin∠ADC=$\frac{AC}{AD}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查了解直角三角形,圆周角定理的应用,能求出∠ACB=90°和∠ABC=∠ADC是解此题的关键.

练习册系列答案
相关题目
 若a、b在数轴上的表示如图:则化简2|a|-|b|+|a+b|-|a-b|的结果是b.
若a、b在数轴上的表示如图:则化简2|a|-|b|+|a+b|-|a-b|的结果是b.
 如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为16cm,求△ABC的周长.
如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为16cm,求△ABC的周长.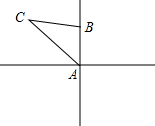 如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )
如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )