题目内容
9.当x取何值时,代数式-12x2-3x-5的值最大,并求出这个最大值.分析 先利用配方法得到:-12x2-3x-5=-12(x+$\frac{1}{8}$)2-$\frac{77}{16}$,再根据非负数的性质得-12(x+$\frac{1}{8}$)2≤0,由此得到当x=$\frac{1}{8}$时,代数式有最大值-$\frac{77}{16}$.
解答 解:-12x2-3x-5=-12(x2+$\frac{1}{4}$x+$\frac{1}{64}$-$\frac{1}{64}$)-5
=-12(x+$\frac{1}{8}$)2-$\frac{77}{16}$,
∵12(x+$\frac{1}{8}$)2≥0,
∴-12(x+$\frac{1}{8}$)2≤0,
∴-12(x+$\frac{1}{8}$)2-$\frac{77}{16}$≤-$\frac{77}{16}$,
∴当x取$\frac{1}{8}$时,这个代数式的值最大,最大的值是-$\frac{77}{16}$.
点评 本题考查了配方法的应用:用配方法解一元二次方程,配方法的理论依据是公式a2±2ab+b2=(a±b)2;利用配方法求二次三项式是一个完全平方式时所含字母系数的值.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
19.下列各组命题不成立的是( )
| A. | 平行四边形的对边平行且相等 | |
| B. | 依次连结矩形各边中点所得的四边形是菱形 | |
| C. | 三角形的重心是三条中线的交点 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
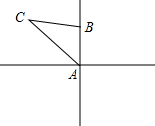 如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )
如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )