题目内容
2.先化简,再求值:(x-1-$\frac{3}{x+1}$)÷$\frac{{x}^{2}+4x+4}{x+1}$,其中x=(π-1)0-(-$\frac{1}{4}$)-1.分析 首先将括号里面通分进而利用分式除法运算法则计算,再化简得出x的值,进而得出答案.
解答 解:原式=$\frac{{x}^{2}-1-3}{x+1}$÷$\frac{{x}^{2}+4x+4}{x+1}$
=$\frac{(x-2)(x+2)}{x+1}$×$\frac{x+1}{(x+2)^{2}}$
=$\frac{x-2}{x+2}$,
∵x=(π-1)0-(-$\frac{1}{4}$)-1
=1+4
=5,
∴原式=$\frac{5-2}{5+2}$=$\frac{3}{7}$.
点评 此题主要考查了分式的化简求值,正确掌握分式的混合运算法则是解题关键.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目

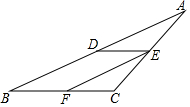 如图,已知DE∥BC,EF平分∠CED,∠A=∠CFE,那么EF与AB平行吗?为什么?
如图,已知DE∥BC,EF平分∠CED,∠A=∠CFE,那么EF与AB平行吗?为什么?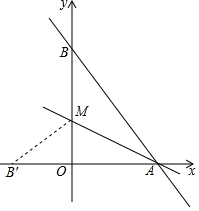 直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则M的坐标为(0,3).
直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则M的坐标为(0,3).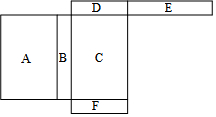 如图是一个长方体的表面展开图,每个面内都标出了字母,请根据要求回答问题.
如图是一个长方体的表面展开图,每个面内都标出了字母,请根据要求回答问题.