题目内容
7.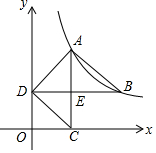 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A(2,4),B(m,n)(m>2)两点,作AC∥y轴交x轴于C,BD∥x轴交y轴于D,AC与BD相交于E,连接AB、AD、CD.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A(2,4),B(m,n)(m>2)两点,作AC∥y轴交x轴于C,BD∥x轴交y轴于D,AC与BD相交于E,连接AB、AD、CD.(1)求反比例函数解析式;
(2)若△ABD的面积等于4,求点B的坐标;
(3)求证:AB∥CD.
分析 (1)把A的坐标代入函数解析式,即可求出答案;
(2)根据三角形面积公式得出$\frac{1}{2}$m(4-n)=2,求出4m-mn=8,把B的坐标代入反比例函数y=$\frac{8}{x}$,即可求出mn=8,求出m、n,即可得出答案;
(3)解直角三角形求出∠ABE=∠CDE,根据平行线的判定得出即可.
解答 解:(1)∵把A(2,4)代入y=$\frac{k}{x}$得:k=8,
∴反比例函数解析式是y=$\frac{8}{x}$;
(2)∵AC∥y轴,BD∥x轴,
∴四边形OCED为平行四边形,
∴∠CDE=∠COD=90°,
∴∠AEB=90°,
∴$\frac{1}{2}$BD×AE=4,
∴$\frac{1}{2}$m(4-n)=2,
∴4m-mn=8,
∵B(m,n)在反比例函数y=$\frac{8}{x}$的图象上,
∴n=$\frac{8}{m}$,
∴mn=8,
∴4m-8=8,
解得:m=4,
∴n=2,
即点B坐标是(4,2);
(3)∵tanB=$\frac{AE}{BE}$=$\frac{4-n}{m-2}$=$\frac{4-\frac{8}{m}}{m-2}$=$\frac{4}{m}$,
tan∠CDE=$\frac{CE}{DE}$=$\frac{n}{2}$=$\frac{\frac{8}{m}}{2}$=$\frac{4}{m}$,
∴tanB=tan∠CDE,
∴∠B=∠CDE,
∴AB∥CD.
点评 本题考查了用待定系数法求反比例函数的解析式,解直角三角形,平行线的判定等知识点,能综合运用知识点进行计算是解此题的关键.

练习册系列答案
相关题目
15.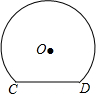 如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为$\frac{10}{3}$m,弦CD=4m,那么隧道的最高处到CD的距离是( )
如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为$\frac{10}{3}$m,弦CD=4m,那么隧道的最高处到CD的距离是( )
 如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为$\frac{10}{3}$m,弦CD=4m,那么隧道的最高处到CD的距离是( )
如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为$\frac{10}{3}$m,弦CD=4m,那么隧道的最高处到CD的距离是( )| A. | $\frac{8}{3}$m | B. | 4m | C. | $\frac{17}{3}$m | D. | 6m |
17.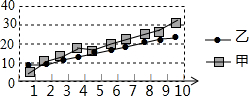 某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )
某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )
 某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )
某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )| A. | 甲得分的平均数小于乙得分的平均数 | |
| B. | 甲得分的中位数小于乙得分的中位数 | |
| C. | 甲得分的方差大于乙得分的方差 | |
| D. | 甲得分的最小值大于乙得分的最小值 |
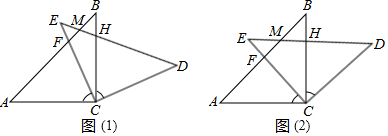
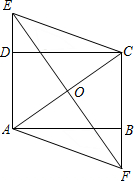 如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E、F,连结AF、CE.
如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E、F,连结AF、CE. 王阿姨销售草莓,草莓成本价为每千克10元,她发现当销售单价为每千克至少10元,但不高于每千克20元时,销售量y(千克)与销售单价x(元)的函数图象如图所示:
王阿姨销售草莓,草莓成本价为每千克10元,她发现当销售单价为每千克至少10元,但不高于每千克20元时,销售量y(千克)与销售单价x(元)的函数图象如图所示: