题目内容
1.已知二次函数y=x2-x-2的图象和x轴相交于点A、B,与y轴相交于点C,过直线BC的下方抛物线上一动点P作PQ∥AC交线段BC于点Q,再过P作PE⊥x轴于点E,交BC于点D.(1)求直线AC的解析式;
(2)求△PQD周长的最大值;
(3)当△PQD的周长最大时,在y轴上有两个动点M、N(M在N的上方),且MN=1,求PN+MN+AM的最大值.
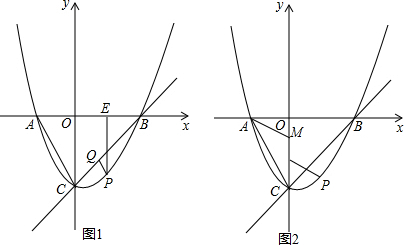
分析 (1)先求出A、C两点坐标,利用待定系数法即可解决问题.
(2)首先证明△PDQ是等腰直角三角形,推出PD最长时,△PDQ的周长最大,设P(m,m2-m-2),则D(m,m-2),可得PD=m-2-(m2-m-2)=-m2+2m=-(m-1)2+1,根据二次函数的性质即可解决问题.
(3)如图2中,作PP′∥y轴,使得PP′=MN=1,连接AP′交y轴于M,此时PN+NM+AM的值最小.求出直线AP′的解析式,求出点M、N的坐标即可解决问题.
解答 解:(1)对于二次函数y=x2-x-2,令x=0得y=-2,令y=0,得x2-x-2=0,解得x=-1或2,
∴A(-1,0),B(2,0),C(0,-2),
设直线AC的解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=-2}\\{-k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=-2}\end{array}\right.$,
∴直线AC的解析式为y=-2x-2.
(2)∵B(2,0),C(0,-2),
∴直线BC的解析式为y=x-2,OB=OC=2,
∴∠OCB=∠OBC=45°,
∵PE⊥x轴,
∴∠DEB=90°,
∴∠EDB=∠QDP=∠EBD=45°,
∵PQ⊥BC,
∴△PDQ是等腰直角三角形,
∴PD最长时,△PDQ的周长最大,设P(m,m2-m-2),则D(m,m-2),
∴PD=m-2-(m2-m-2)=-m2+2m=-(m-1)2+1,
∵-1<0,
∴m=1时,PD的值最大,PD最大值为1,此时DQ=PQ=$\frac{\sqrt{2}}{2}$,
∴△PDQ的周长的最大值为1+$\sqrt{2}$.
(3)如图2中,作PP′∥y轴,使得PP′=MN=1,连接AP′交y轴于M,此时PN+NM+AM的值最小.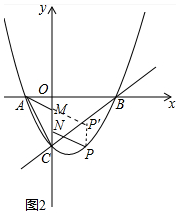
由(2)可知P(1,-2),
∴P′(1,-1),∵A(-1,0),
∴直线AP′的解析式为y=-$\frac{1}{2}$x-$\frac{1}{2}$,
∴M(0,-$\frac{1}{2}$),N(0,-$\frac{3}{2}$),
∴AM=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$,PN=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$,
∴AM+MN+PN的最小值为$\sqrt{5}$+1.
点评 本题考查二次函数综合题、一次函数的应用、两点之间线段最短、勾股定理等知识,解题的关键是学会构建二次函数解决最值问题,学会利用两点之间线段最短解决最短问题,属于中考压轴题.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案 如图,在圆内接四边形ABCD中,若∠A=68°,则∠C=112°.
如图,在圆内接四边形ABCD中,若∠A=68°,则∠C=112°.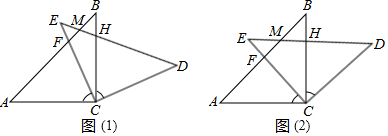
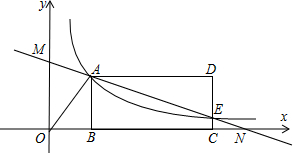 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(3,0),tan∠AOB=$\frac{4}{3}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(3,0),tan∠AOB=$\frac{4}{3}$.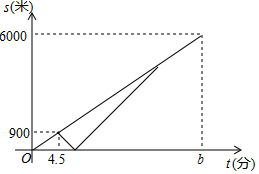 周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园,两人同时从学校出发,以a米/分的速度匀速行驶,出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙,甲追上乙后,两人以相同的速度前往净月潭,乙骑自行车的速度始终不变,设甲,乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.
周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园,两人同时从学校出发,以a米/分的速度匀速行驶,出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙,甲追上乙后,两人以相同的速度前往净月潭,乙骑自行车的速度始终不变,设甲,乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.