题目内容

7．有四张不透明的卡片，正面分别写有下列函数关系式：y=$\frac{1}{x}$；y=-x；y=x2；y=2x+1，除正面的函数关系式不同外，其余都相同，将它们背面朝上洗匀后，从中抽取一张，则抽到的函数图象不经过第四象限的概率是$\frac{3}{4}$．

分析 利用反比例函数、一次函数和二次函数的性质可判断函数y=$\frac{1}{x}$，y=2x+1，y=x2的图象不经过第四象限，然后根据概率公式可求出抽到的函数图象不经过第四象限的概率．

解答 解：下列函数关系式：y=$\frac{1}{x}$；y=-x；y=x2；y=2x+1中，函数y=$\frac{1}{x}$，y=2x+1，y=x2的图象不经过第四象限，
所以函数图象不经过第四象限的概率=$\frac{3}{4}$．

点评 本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．

练习册系列答案
相关题目
17．在同一平面直角坐标系中，请按要求完成下面问题：
（1）△ABC的各定点坐标分别为A（1，1），B（-3，-1），C（-3，1），请画出它的外接圆⊙P，并写出圆心P点的坐标；
（2）将△ABC绕点B逆时针旋转90°得到△A′BC′，请画出△A′BC′．
18．式子（x-3）0+$\sqrt{x}$有意义，则x的取值范围是（　　）
A．x≠3B．x≥0C．x≠3或x≥0D．x≠3且x≥0
15．如图，一块直角边分别为6cm和8cm的三角形木板，绕6cm的边旋转一周，则斜边扫过的面积是（　　）
A．48πcm2B．60πcm2C．80πcm2D．90πcm2
2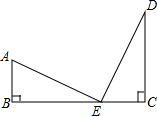．如图所示，Rt△ABE≌Rt△ECD，点B、E、C在同一直线上，则结论：①AE=ED；②AE⊥DE；③BC=AB+CD；④AB∥DC中成立的是（　　）
A．仅①B．仅①③C．仅①③④D．仅①②③④
12．下列等式的变形中，正确的是（　　）
①若x+3=16，则x+6=19
②若a+b=c+d，则a+2b+c=b+2c+d
③若3a=4b，则3ac=4bc
④若3a=4b，则$\frac{3a}{{x}^{2}+1}$=$\frac{4b}{{x}^{2}+1}$．
A．①B．①③C．①③④D．①②③④
19．如果2a+b=0（a≠0），则|$\frac{a}{|b|}$-1|+|$\frac{|a|}{b}$-2|的值为（　　）
A．1或2B．2或3C．3D．4
16．已知关于x的一元二次方程x2-2x+k=0．
（1）若方程有实数根，求k的取值范围；
（2）如果k是满足条件的最大的整数，且方程x2-2x+k=0一根的相反数是一元二次方程（m-1）x2-3mx-7=0的一个根，求m的值及这个方程的另一根．
17．（1）计算：-23+$\sqrt{27}$-|2-3$\sqrt{3}$|
（2）解方程：x2-4x-2=0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网