题目内容
17.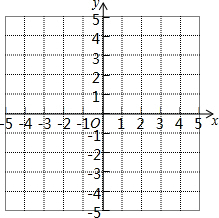 在同一平面直角坐标系中,请按要求完成下面问题:
在同一平面直角坐标系中,请按要求完成下面问题:(1)△ABC的各定点坐标分别为A(1,1),B(-3,-1),C(-3,1),请画出它的外接圆⊙P,并写出圆心P点的坐标;
(2)将△ABC绕点B逆时针旋转90°得到△A′BC′,请画出△A′BC′.
分析 (1)作AC和BC的垂直平分线得到点P,然后以点P为圆心,PA为半径作⊙P,则⊙P为△ABC的外接圆,再写出P点坐标;
(2)利用网格特点和旋转的性质,画出点A、C的对应点A′、C′即可得到△A′BC′.
解答 解:(1)如图,⊙P为所作,P点坐标为(-1,0);
(2)如图,△A′BC′为所作.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了复杂作图.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
7.把分式$\frac{2a}{a+b}$中的a、b都扩大5倍,则分式的值( )
| A. | 扩大10倍 | B. | 不变 | C. | 扩大5倍 | D. | 缩小5倍 |
8.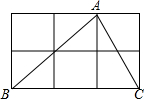 如图,△ABC的3个顶点分别在小正方形的顶点上,这样的三角形叫做格点三角形,在图中再画格点三角形(位置不同于△ABC),使得所画三角形与△ABC全等,则这样的格点三角形能画( )
如图,△ABC的3个顶点分别在小正方形的顶点上,这样的三角形叫做格点三角形,在图中再画格点三角形(位置不同于△ABC),使得所画三角形与△ABC全等,则这样的格点三角形能画( )
 如图,△ABC的3个顶点分别在小正方形的顶点上,这样的三角形叫做格点三角形,在图中再画格点三角形(位置不同于△ABC),使得所画三角形与△ABC全等,则这样的格点三角形能画( )
如图,△ABC的3个顶点分别在小正方形的顶点上,这样的三角形叫做格点三角形,在图中再画格点三角形(位置不同于△ABC),使得所画三角形与△ABC全等,则这样的格点三角形能画( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5. 如图,二次函数y=ax2+bx+c(a≠0)的图象过(-2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0,其中正确结论的个数是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象过(-2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0,其中正确结论的个数是( )
 如图,二次函数y=ax2+bx+c(a≠0)的图象过(-2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0,其中正确结论的个数是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象过(-2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0,其中正确结论的个数是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
12.在平面直角坐标系中,点P(-2,3)与点Q关于原点对称,则点Q的坐标为( )
| A. | (-2,-3) | B. | (3,-2) | C. | (2,3) | D. | (2,-3) |
9.下列各数中,属于无理数的是( )
| A. | -$\frac{π}{2}$ | B. | $\frac{22}{7}$ | C. | 0.1010010001 | D. | 0 |