题目内容
10.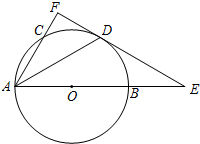 如图,AB是⊙O的直径,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
如图,AB是⊙O的直径,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.(1)求证:AF⊥EF;
(2)若tan∠CAD=$\frac{1}{2}$,AB=5,求线段BE的长.
分析 (1)连结OD,由直线EF与⊙O相切于点D,得到OD⊥EF,由同圆的半径相等推出∠1=∠3,由点D为$\widehat{BC}$的中点,得到∠1=∠2,证得∠2=∠3,得到OD∥AF,得出结论AF⊥EF;
(2)连结BD,通过解直角三角形得到BD=$\sqrt{5}$,AD=$2\sqrt{5}$,DF=2,AF=4,由三角形相似列比例式求解.
解答 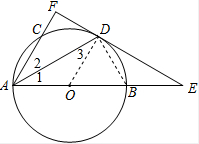 (1)证明:连结OD,
(1)证明:连结OD,
∵直线EF与⊙O相切于点D,
∴OD⊥EF,
∵OA=OD,
∴∠1=∠3,
∵点D为$\widehat{BC}$的中点,
∴∠1=∠2,
∴∠2=∠3,
∴OD∥AF,
∴AF⊥EF;
(2)解:连结BD,
∵$tan∠CAD=\frac{1}{2}$,
∴$tan∠1=\frac{1}{2}$,
在Rt△ADB中,AB=5,
∴BD=$\sqrt{5}$,AD=$2\sqrt{5}$,
在Rt△AFD中,可得DF=2,AF=4,
∵OD∥AF,
∴△EDO∽△EFA,
∴$\frac{OD}{AF}=\frac{OE}{AE}$,
又∵OD=2.5,设BE=x,
∴$\frac{2.5}{4}=\frac{2.5+x}{5+x}$,
∴$x=\frac{5}{3}$,即BE=$\frac{5}{3}$.
点评 本题考查了切线的性质,圆周角定理,解直角三角形,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 如图,二次函数y=ax2+bx+c的图象经过点(-1,0)、(3,0)和(0,2),当x=2时,y的值为2.
如图,二次函数y=ax2+bx+c的图象经过点(-1,0)、(3,0)和(0,2),当x=2时,y的值为2. 如图,在△ABC中,∠A=30°,∠B=45°,BC=$\sqrt{6}$,求AB的长.
如图,在△ABC中,∠A=30°,∠B=45°,BC=$\sqrt{6}$,求AB的长.