题目内容
9.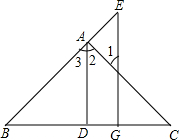 如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,可得AD平分∠BAC,理由如下:
如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,可得AD平分∠BAC,理由如下:∵AD⊥BC于点D,EG⊥BC于点G(已知),
∴∠ADC=∠EGB=90°垂直的定义
∴∠ADC+∠EGB=180°等式的性质
∴AD∥EG同旁内角互补,两直线平行
∴∠1=∠2两直线平行,内错角相等
∠E=∠3两直线平行,同位角相等
又∵∠E=∠1(已知)
∴∠2=∠3(等量代换)
∴AD平分∠BAC角平分线的定义.
分析 先利用同位角相等,两直线平行求出AD∥EG,再利用平行线的性质求出∠1=∠2,∠E=∠3和已知条件等量代换求出∠2=∠3即可证明.
解答 解:∵AD⊥BC于D,EG⊥BC于G,(已知)
∴∠ADC=∠EGB=90°,(垂直的定义)
∴∠ADC+∠EGB=180°,(等式的性质)
∴AD∥EG,(同旁内角互补,两直线平行)
∴∠1=∠2,(两直线平行,内错角相等)
∠E=∠3,(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3(等量代换)
∴AD平分∠BAC(角平分线的定义).
故答案为:垂直的定义;等式的性质;同旁内角互补,两直线平行;两直线平行,内错角相等;∠E;两直线平行,同位角相等;∠2;∠3;等量代换;角平分线的定义.
点评 本题考查平行线的判定与性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.

练习册系列答案
相关题目
18.下列调查中,适合采用全面调查(普查)方式的是( )
| A. | 了解一批节能灯泡的使用寿命 | |
| B. | 了解某班同学“跳绳”的成绩 | |
| C. | 了解全国每天丢弃的塑料袋的数量 | |
| D. | 了解上海卫视“今晚80后”栏目的收视率 |
17.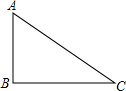 △ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )
△ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )
 △ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )
△ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )| A. | $2\sqrt{5}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 4 |
 如图所示,要使a∥b,需要添加一个条件,这个条件可以是∠1=∠3(答案不唯一).
如图所示,要使a∥b,需要添加一个条件,这个条件可以是∠1=∠3(答案不唯一).




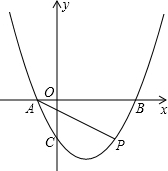 设抛物线$y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-2$与x轴的交点为A(x1,0),B(x2,0),其中x1< x2,点P(m,n)为抛物线上一动点,连接AP,BP,当∠APB为锐角时,下列m的取值范围中正确的是①③⑤;(填序号)
设抛物线$y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-2$与x轴的交点为A(x1,0),B(x2,0),其中x1< x2,点P(m,n)为抛物线上一动点,连接AP,BP,当∠APB为锐角时,下列m的取值范围中正确的是①③⑤;(填序号)