题目内容
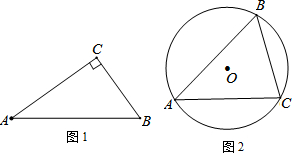
5. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C,tan∠BAC=2.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C,tan∠BAC=2.(1)求抛物线的解析式;
(2)点P从O点出发,在线段OB上以每秒1个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度向C点运动,其中一个点到达终点时,另一点也停止运动,问运动多少秒时,△PBQ的面积最大?最大面积是多少?
(3)过点P向x轴作垂线,交抛物线于一点M,是否存在点M,使得点M到BC的距离等于$\frac{3\sqrt{2}}{4}$?若存在,求出点M的坐标;若不存在,请说明理由.
分析 (1)把点A、B、C的坐标分别代入抛物线解析式,列出关于系数a、b的解析式,通过解方程组求得它们的值;
(2)设运动时间为t秒.利用三角形的面积公式列出S△PBQ与t的函数关系式S△PBQ=-$\frac{\sqrt{2}}{4}$(t-2)2+$\sqrt{2}$,利用二次函数的图象性质进行解答;
(3)首先求出MN的长,进而得出MN=(t-4)-($\frac{1}{2}$t2-t-4),求出符合题意的答案即可.
解答  解:(1)∵tan∠BAC=2,∴OC=2OA=4,∴C(0,-4)
解:(1)∵tan∠BAC=2,∴OC=2OA=4,∴C(0,-4)
将A(-2,0)、B(4,0)、C(0,-4)三点坐标分别代入y=ax2+bx+c,
得$\left\{\begin{array}{l}{4a-2b+c=0}\\{16+4b+c=0}\\{c=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-1}\\{c=-4}\end{array}\right.$
∴抛物线的解析式为:y=$\frac{1}{2}$x2-x-4;
(2)设运动时间为t秒,由题意可知:0<t<4,
则OP=t,PB=4-t,BQ=t,
过点Q作QD⊥AB,垂直为D,
∵OC=4,OB=4,∴∠OBC=45°,∴DQ=$\frac{\sqrt{2}}{2}$t,
∴S△PBQ=$\frac{1}{2}$PB•DQ=$\frac{1}{2}$(4-t)×$\frac{\sqrt{2}}{2}$t=-$\frac{\sqrt{2}}{4}$t2+$\sqrt{2}$t=-$\frac{\sqrt{2}}{4}$(t-2)2+$\sqrt{2}$,
∴当运动2秒时,△PBQ面积最大,最大值为$\sqrt{2}$;
(3)假设存在点M,使得点M到BC的距离MH=$\frac{3\sqrt{2}}{4}$,
如图,设PM交直线BC于点N,易得∠HMN=45°,则MN=$\sqrt{2}$MH=$\frac{3\sqrt{2}}{4}$•$\sqrt{2}$=$\frac{3}{2}$,
设直线BC的关系式为y=kx-d,
则$\left\{\begin{array}{l}{4k+d=0}\\{d=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{d=-4}\end{array}\right.$,
故直线BC的关系式为:y=x-4,
所以N点坐标为(t,t-4),M点坐标为(t,$\frac{1}{2}$t2-t-4),
∴MN=(t-4)-($\frac{1}{2}$t2-t-4),
∴(t-4)-($\frac{1}{2}$t2-t-4)=$\frac{3}{2}$,
解得:t1=1,t2=3,
故t=1时,$\frac{1}{2}$t2-t-4=-$\frac{9}{2}$,t=3时,$\frac{1}{2}$t2-t-4=-$\frac{5}{2}$,
所以存在点M满足条件,坐标为:(1,-$\frac{9}{2}$),(3,-$\frac{5}{2}$).
点评 此题主要考查了二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式,表示出线段MN的长是解题关键.

| A. | 了解一批节能灯泡的使用寿命 | |
| B. | 了解某班同学“跳绳”的成绩 | |
| C. | 了解全国每天丢弃的塑料袋的数量 | |
| D. | 了解上海卫视“今晚80后”栏目的收视率 |
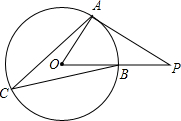 如图,PA为⊙O的切线,A为切点,B是OP与⊙O的交点,C是优弧AB上一点(不与点A、B重合).若∠P=36°,则∠ACB的大小为( )
如图,PA为⊙O的切线,A为切点,B是OP与⊙O的交点,C是优弧AB上一点(不与点A、B重合).若∠P=36°,则∠ACB的大小为( )| A. | 18° | B. | 27° | C. | 36° | D. | 54° |
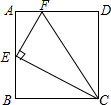 如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )①∠AEF=∠BCE;②AF+BC>CF;③S△CEF=S△EAF+S△CBE;④若$\frac{BC}{CD}$=$\frac{\sqrt{3}}{2}$,则△CEF≌△CDF.
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
 小明在学校九年级中随机选取部分同学对“你最喜欢的球类运动”进行问卷调查,调查结果如图所示.则选择每种球类人数的众数与中位数分别是( )
小明在学校九年级中随机选取部分同学对“你最喜欢的球类运动”进行问卷调查,调查结果如图所示.则选择每种球类人数的众数与中位数分别是( )| A. | 16,14 | B. | 16,10 | C. | 14,14 | D. | 14,10 |
 △ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )
△ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )| A. | $2\sqrt{5}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 4 |