题目内容
如图,已知在△ABC中,AD是BC边上的中线,以AB为直径的⊙O交BC于点D,过D作MN⊥AC于点M,交AB的延长线于点N,过点B作BG⊥MN于G.
(1)求证:△BGD∽△DMA;
(2)求证:直线MN是⊙O的切线.
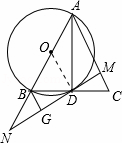
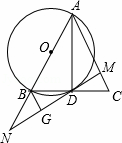
证明:(1)∵MN⊥AC于点M,BG⊥MN于G,
∴∠BGD=∠DMA=90°.
∵以AB为直径的⊙O交BC于点D,∴AD⊥BC,∠ADC=90°,
∴∠ADM+∠CDM=90°,
∵∠DBG+∠BDG=90°,∠CDM=∠BDG,
∴∠DBG=∠ADM.
在△BGD与△DMA中, ,∴△BGD∽△DMA;
,∴△BGD∽△DMA;
(2)连结OD.∵BO=OA,BD=DC,
∴OD是△ABC的中位线,∴OD∥AC.∵MN⊥AC,BG⊥MN,
∴AC∥BG,∴OD∥BG,∵BG⊥MN,∴OD⊥MN,
∴直线MN是⊙O的切线.

练习册系列答案
相关题目

 >–b–c
>–b–c x2-
x2- 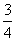 x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C。
x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C。
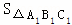 :
: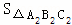 = (不写解答过程,直接写出结果).
= (不写解答过程,直接写出结果).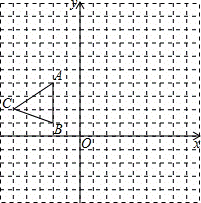
 B.
B.  C.
C.  D.
D. 

 边形的一个外角等于40°.则
边形的一个外角等于40°.则