题目内容
如图，在平面直角坐标系xOy中，△ABC三个顶点坐标分别为A（﹣2，4），B（﹣2，1），C（﹣5，2）．
（1）请画出△ABC关于x轴对称的△A1B1C1．
（2）将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以﹣2，得到对应的点A2，B2，C2，请画出△A2B2C2．
（3）求△A1B1C1与△A2B2C2的面积比，即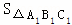
：
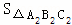= （不写解答过程，直接写出结果）．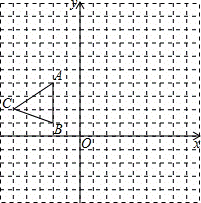
解：（1）如图所示：△A1B1C1即为所求；
（2）如图所示：△A2B2C2即为所求；
（3）∵将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以﹣2，得到对应的点A2，B2，C2，
∴△A1B1C1与△A2B2C2的相似比为：1：2，
∴
：
=1：4．故答案为：1：4．
练习册系列答案
相关题目
，求⊙O的面积。
﹣
=2有增根，则这个增根是 ．
七（一）班同学为了解某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据整理如下表（部分）：
| 月均用水量x/m3 | 0＜x≤5 | 5＜x≤10 | 10＜x≤15 | 15＜x≤20 | x＞20 |
| 频数/户 | 12 | 20 | 3 | ||
| 频率 | 0.12 | 0.07 |
若该小区有800户家庭，据此估计该小区月均用水量不超过10m3的家庭约有 户．
