题目内容
如图8,已知抛物线y=  x2-
x2- 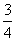 x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C。
x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C。
(1)直接写出A、D、C三点的坐标;
(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;
(3)设点C关于抛物线对称的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由。
解:(1)A(4,0) 、D(-2,0)、C(0,-3)
(2)连接AC,与抛物线的对称轴交点M即为所求,直线AC的解析式y= -3,
-3,
对称轴是直线x= =1,把x=1代入y=
=1,把x=1代入y= -3得y=-
-3得y=-
`∴M(1,- )
)
(3)如下图,当点P与D重合时,四边形ADCB是梯形,此时点P为(-2,0);
直线AB的解析式为y= ,过点C作CP1//AB,与抛物线交于点P1,
,过点C作CP1//AB,与抛物线交于点P1,
直线CP1的解析式为y= ,联立y=
,联立y=  x2-
x2- 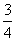 x-3,可得P1(6,6)
x-3,可得P1(6,6)




练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
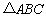 的三个顶点均在格点上,则
的三个顶点均在格点上,则 ( ).
( ). (B)
(B) (C)
(C) (D)
(D)

 方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45
方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45 方向
方向 上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
 ,求⊙O的面积。
,求⊙O的面积。

 ﹣
﹣ =2有增根,则这个增根是 .
=2有增根,则这个增根是 .
 = .
= .