题目内容
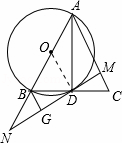
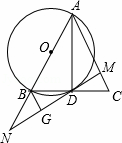
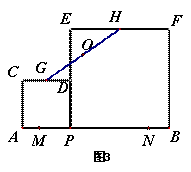
如图，∠ABC=90°，D、E分别在BC、AC上，AD⊥DE，且AD=DE，点F是AE的中点，FD与AB相交于点M．
（1）求证：∠FMC=∠FCM；
（2）AD与MC垂直吗？并说明理由．
（1）证明：∵△ADE是等腰直角三角形，F是AE中点，
∴DF⊥AE，DF=AF=EF，又∵∠ABC=90°，∠DCF，∠AMF都与∠MAC互余，
∴∠DCF=∠AMF，
在△DFC和△AFM中，
，∴△DFC≌△AFM（AAS），
∴CF=MF，∴∠FMC=∠FCM；
（2）AD⊥MC，
理由：由（1）知，∠MFC=90°，FD=EF，FM=FC，∴∠FDE=∠FMC=45°，
∴DE∥CM，∴AD⊥MC．
练习册系列答案
相关题目
有解，则实数a的取值范围是（ ）七（一）班同学为了解某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据整理如下表（部分）：
| 月均用水量x/m3 | 0＜x≤5 | 5＜x≤10 | 10＜x≤15 | 15＜x≤20 | x＞20 |
| 频数/户 | 12 | 20 | 3 | ||
| 频率 | 0.12 | 0.07 |
若该小区有800户家庭，据此估计该小区月均用水量不超过10m3的家庭约有 户．
= .
，a3=
，…，an=
，则a1+a2+a3+…+a2014= ．