题目内容
18.若$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{d}$=$\frac{d}{a}$,求$\frac{a-b+c-d}{a+b-c+d}$的值.分析 根据等比性质,可得a=bk,b=ck,c=dk,d=ak,根据等量代换,可得关于k的方程,根据开方运算,可得k的值,根据分式的性质,可得答案.
解答 解:设$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{d}$=$\frac{d}{a}$=k,得
a=bk,b=ck,c=dk,d=ak,
a=ck•k=dk•k•k=ak•k•k•k=ak4,
∵a≠0,
∴k4=1,解得k=1或k=-1.
当k=1时,a=b=c=d,$\frac{a-b+c-d}{a+b-c+d}$=$\frac{a-a+a-a}{a+a-a+a}$=0;
当k=-1时,a=-b,-b=c,c=-d,-d=a,
b=-a,c=a,d=-a,
$\frac{a-b+c-d}{a+b-c+d}$=$\frac{a+a+a+a}{a-a-a-a}$=$\frac{4a}{-2a}$=-2
点评 本题考查了比例的性质,利用了等比性质,利用等量代换得出关于k的方程是解题关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
13.方程(x-2)(x-3)=6的两根分别为( )
| A. | 2或3 | B. | 5或0 | C. | 5或1 | D. | 4或6 |
10. 如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,OA=2,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,OA=2,则图中阴影部分的面积为( )
 如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,OA=2,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,OA=2,则图中阴影部分的面积为( )| A. | $\frac{4π}{3}$-$\sqrt{3}$ | B. | $\frac{4π}{3}$-2$\sqrt{3}$ | C. | π-$\sqrt{3}$ | D. | $\frac{π}{3}$-$\frac{\sqrt{3}}{4}$ |
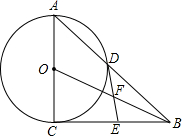 如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交斜边于点D,点E为BC上一点,BE=DE,连接OB交DE于点F.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交斜边于点D,点E为BC上一点,BE=DE,连接OB交DE于点F. 如图正方形ABCD中,CF:CD=1:3,CE:CB=1:3,求四边形ABGD的面积与正方形ABCD的面积之比.
如图正方形ABCD中,CF:CD=1:3,CE:CB=1:3,求四边形ABGD的面积与正方形ABCD的面积之比. 我们知道,对于一些立体图形问题,常把它转化为平面图形来研究和处理,棱长为a的正方体摆成如图所示的形状,问:
我们知道,对于一些立体图形问题,常把它转化为平面图形来研究和处理,棱长为a的正方体摆成如图所示的形状,问: