题目内容
4. 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=40°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=40°,则∠P的度数为( )| A. | 100° | B. | 110° | C. | 80° | D. | 90° |
分析 由条件可证明△AMK≌△BKN,再结合外角的性质可求得∠A=∠MKN,再利用三角形内角和可求得∠P.
解答 解:
∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中
$\left\{\begin{array}{l}{AM=BK}\\{∠A=∠B}\\{AK=BN}\end{array}\right.$
∴△AMK≌△BKN(SAS),
∴∠AMK=∠BKN,
∵∠A+∠AMK=∠MKN+∠BKN,
∴∠A=∠MKN=40°,
∴∠P=180°-∠A-∠B=180°-40°-40°=100°,
故选A.
点评 本题主要考查全等三角形的判定和性质及三角形内角和定理,利用条件证得△AMK≌△BKN是解题的关键.

练习册系列答案
相关题目
5.下列方程是二元一次方程的是( )
| A. | 3x+y+z=9 | B. | x2-y2=1 | C. | 3x+y=8 | D. | 7x+2=8 |
12. 如图,某计算装置有一数据输入口A和一运算结果的输出口B,如表是小明输入的一些数据和这些数据经该装置计算后输出的相应结果:按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
如图,某计算装置有一数据输入口A和一运算结果的输出口B,如表是小明输入的一些数据和这些数据经该装置计算后输出的相应结果:按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
 如图,某计算装置有一数据输入口A和一运算结果的输出口B,如表是小明输入的一些数据和这些数据经该装置计算后输出的相应结果:按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
如图,某计算装置有一数据输入口A和一运算结果的输出口B,如表是小明输入的一些数据和这些数据经该装置计算后输出的相应结果:按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )| A | 1 | 2 | 3 | 4 | 5 |
| B | 2 | 5 | 10 | 17 | 26 |
| A. | 21 | B. | 29 | C. | 99 | D. | 101 |
19. 三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大圆的直径,则图中阴影部分的面积为( )
三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大圆的直径,则图中阴影部分的面积为( )
 三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大圆的直径,则图中阴影部分的面积为( )
三个圆的位置如图所示,m,n分别是两个较小的圆的直径,m+n是最大圆的直径,则图中阴影部分的面积为( )| A. | 2πmn | B. | $\frac{1}{2}$πmn | C. | π(m+n) | D. | πmn |
9.有理数a、b满足a2b2+a2+b2-4ab+1=0,则a、b的值分别为( )
| A. | a=1,b=1 | B. | a=-1,b=-1 | C. | a=b=1或a=b=-1 | D. | 不能确定 |
13.在平面直角坐标系中,点(3,-4)关于原点对称的点的坐标是( )
| A. | (3,4) | B. | (-3,-4) | C. | (-3,4) | D. | (-4,3) |
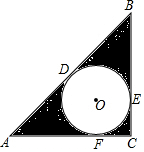 如图,⊙O是Rt△ABC的内切圆,与△ABC的切点分别为D、E、F,∠C=90°,AB=5,AC=4,求图中阴影部分的面积.
如图,⊙O是Rt△ABC的内切圆,与△ABC的切点分别为D、E、F,∠C=90°,AB=5,AC=4,求图中阴影部分的面积. 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=5,试求CD的长.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=5,试求CD的长.