Question

6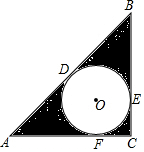．如图，⊙O是Rt△ABC的内切圆，与△ABC的切点分别为D、E、F，∠C=90°，AB=5，AC=4，求图中阴影部分的面积．

Answer 1

分析 根据勾股定理求出BC，求出Rt△ABC的内切圆⊙O的半径，结合图形计算即可．

解答 解：∵∠C=90°，AB=5，AC=4，
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=3，
则Rt△ABC的内切圆⊙O的半径为：$\frac{3+4-5}{2}$=1，
∴阴影部分的面积=$\frac{1}{2}$×3×4-π×1²=6-π．

点评 本题考查的是三角形的内切圆与内心的概念和性质、扇形面积的计算，掌握三角形的内切圆的半径的计算公式是解题的关键．