题目内容
如图1,在平面直角坐标系xOy中,点F(2,2),过函数y=
(x>0,常数k>0)图象上一点A(
,a)作y轴的平行线交直线l:y=-x+2于点C,且AC=AF.
(1)求a的值,并写出函数y=
(x>0)的解析式;
(2)过函数y=
(x>0)图象上任意一点B,作y轴的平行线交直线l于点D,是否总有BD=BF成立?并说明理由;
(3)如图2,若P是函数y=
(x>0)图象上的动点,过点P作x轴的垂线交直线l于点N,分别过点P、N作y的垂线交y轴于点Q、M,问是否存在点P,使得矩形PQMN的周长取得最小值?若存在,请求出此时点P的坐标及矩形PQMN的周长;若不存在,请说明理由.

| k |
| x |
| 1 |
| 2 |
(1)求a的值,并写出函数y=
| k |
| x |
(2)过函数y=
| k |
| x |
(3)如图2,若P是函数y=
| k |
| x |

考点:反比例函数综合题
专题:
分析:(1)求出AC、AF的表达式,根据AC=AF求出a的值,然后利用待定系数法求出a的值即可;
(2)设B(m,
)(m>0),则D(m,-m+2),根据勾股定理求出BF的长即可;
(3)结合(2)可知,当且仅当P、Q、F三点共线时,矩形PQMN的周长取到最小值=2FE=4.
(2)设B(m,
| 2 |
| m |
(3)结合(2)可知,当且仅当P、Q、F三点共线时,矩形PQMN的周长取到最小值=2FE=4.
解答:解:(1)AC=a-
,AF=
,
∵AC=AF,
∴a=4,
∴点A(
,4),
∴k=2,
∴y=
(x>0).
(2)设B(m,
)(m>0),则D(m,-m+2),
∴BD=
-(-m+2)=
+m-2,
BF=
,
∴BD=BF.
(3)答:存在满足题设条件的点P.
解法1:设直线l交y轴于点E,连接EF,QF,由(2)得,PF=PN,
矩形PQMN的周长=2(PN+PQ)=2(PF+PQ),
∵PF+PQ≥QF≥EF,
∴当且仅当P、Q、F三点共线时,矩形PQMN的周长取到最小值=2FE=4,
此时,点P的坐标为(1,2).
解法2:设P(m,
)(m>0),则N(m,-m+2),
∴矩形PQMN的周长=2(PN+PQ)=2(
+m-2+m)=
+4m-4=(
-2
)2+4,
∴当
-2
=0,即m=1,P(1,2)时,矩形PQMN的周长取得最小值为4.
| 3 |
| 2 |
|
∵AC=AF,
∴a=4,
∴点A(
| 1 |
| 2 |
∴k=2,
∴y=
| 2 |
| x |
(2)设B(m,
| 2 |
| m |
∴BD=
| 2 |
| m |
| 2 |
| m |
BF=
(m-2)2+(
|
∴BD=BF.
(3)答:存在满足题设条件的点P.
解法1:设直线l交y轴于点E,连接EF,QF,由(2)得,PF=PN,
矩形PQMN的周长=2(PN+PQ)=2(PF+PQ),
∵PF+PQ≥QF≥EF,
∴当且仅当P、Q、F三点共线时,矩形PQMN的周长取到最小值=2FE=4,
此时,点P的坐标为(1,2).
解法2:设P(m,
| 2 |
| m |
∴矩形PQMN的周长=2(PN+PQ)=2(
| 2 |
| m |
| 4 |
| m |
| 2 | ||
|
| m |
∴当
| 2 | ||
|
| m |
点评:本题考查了反比例函数综合题,涉及勾股定理、存在性问题,综合性很强,要灵活处理,同时注意从多角度解题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
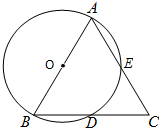 如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.
如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.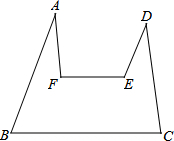 如图,顺次连结A、B、C、D、E、F,若∠F=∠A+∠B.求证:∠E=∠D+∠C.
如图,顺次连结A、B、C、D、E、F,若∠F=∠A+∠B.求证:∠E=∠D+∠C.