题目内容
分数
,
,
,…,
中共有 个分数可以化成混循环小数.
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 40 |
考点:规律型:数字的变化类
专题:规律型
分析:关于
化成混循环小数,n应该是2或5的倍数,而且至少有一个非2非5的质因数.在1,2,…,40中符合以上条件的为6,12,14,15,18,22,24,26,28,30,34,35,36,38,共14个.
| 1 |
| n |
解答:解:6=2×3,12=2×2×3,14=2×7,15=3×5,18=2×3×3,22=2×11,24=2×2×2×3,26=2×13,28=2×2×7,30=2×3×5,34=2×17,35=5×7,36=2×2×3×3,38=2×19.
∴分数
,
,
,…,
中共有14个分数可以化成混循环小数.
故答案为:14.
∴分数
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 40 |
故答案为:14.
点评:本题考查了混循环小数.分数可以化成混循环小数是分数的分母是2或5的倍数,而且至少有一个非2非5的质因数的真分数.

练习册系列答案
相关题目
最接近
的整数是( )
2004+
|
| A、44 | B、45 | C、46 | D、47 |
如图,一条两边平行的纸带的宽度(两平行线间的距离)为8cm,现将纸带折起压平(两条相对的长边应相交),那么重叠部分△ABC面积的最小值为( )


| A、16cm2 |
| B、32cm2 |
| C、64cm2 |
| D、无最小值 |
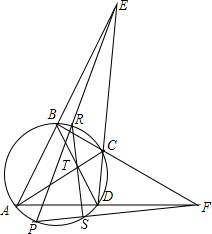 如图,四边形ABCD内接于圆,AB,DC延长线交于E,AD、BC延长线交于F,P为圆上任意一点,PE,PF分别交圆于R,S.若对角线AC与BD相交于T.求证:R,T,S三点共线.
如图,四边形ABCD内接于圆,AB,DC延长线交于E,AD、BC延长线交于F,P为圆上任意一点,PE,PF分别交圆于R,S.若对角线AC与BD相交于T.求证:R,T,S三点共线. 为了庆祝国庆,学校准备在教学楼大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为lm,高为3m.如果要求彩带从柱子底端的A处绕柱子4圈后到达柱子顶端的B处,那么至少应购买彩带
为了庆祝国庆,学校准备在教学楼大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为lm,高为3m.如果要求彩带从柱子底端的A处绕柱子4圈后到达柱子顶端的B处,那么至少应购买彩带