题目内容
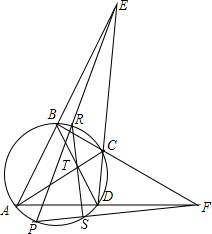如图，四边形ABCD内接于圆，AB，DC延长线交于E，AD、BC延长线交于F，P为圆上任意一点，PE，PF分别交圆于R，S．若对角线AC与BD相交于T．求证：R，T，S三点共线．考点：相似三角形的判定与性质,圆内接四边形的性质
专题：证明题
分析：连接PD，AS，RC，BR，AP，SD．由△EBR∽△EPA，△FDS∽△FPA，知
=
，
=
，则
=
①；又由△ECR∽△EPD，△FPD∽△FAS，知
=
，
=
，则
=
②；由①，②得
=
．故
•
•
=
•
•
③，对△EAD应用梅涅劳斯定理，有
•
•
=1④由③，④得
•
•
=1．由此得到结论．
| BR |
| PA |
| EB |
| EP |
| PA |
| DS |
| FP |
| FD |
| BR |
| DS |
| EB•FP |
| EP•FD |
| CR |
| PD |
| EC |
| EP |
| PD |
| AS |
| FP |
| FA |
| CR |
| AS |
| EC•FP |
| EP•FA |
| BR•AS |
| DS•CR |
| EB•FA |
| EC•FD |
| BR |
| RC |
| CD |
| DS |
| SA |
| AB |
| EB |
| BA |
| AF |
| FD |
| DC |
| CE |
| EB |
| BA |
| AF |
| FD |
| DC |
| CE |
| BR |
| RC |
| CD |
| DS |
| SA |
| AB |
解答：
证明：如图，
连接PD，AS，RC，BR，AP，SD．
由△EBR∽△EPA，△FDS∽△FPA，知
=
，
=
．
两式相乘，得
=
①，
又由△ECR∽△EPD，△FPD∽△FAS，知
=
，
=
．两式相乘，得
=
②，
由①，②得
=
．故
•
•
=
•
•
③，
对△EAD应用梅涅劳斯定理，有
•
•
=1④
由③，④得
•
•
=1．
∴BD，RS，AC交于一点，
所以R，T，S三点共线．
证明：如图，连接PD，AS，RC，BR，AP，SD．
由△EBR∽△EPA，△FDS∽△FPA，知
| BR |
| PA |
| EB |
| EP |
| PA |
| DS |
| FP |
| FD |
两式相乘，得
| BR |
| DS |
| EB•FP |
| EP•FD |
又由△ECR∽△EPD，△FPD∽△FAS，知
| CR |
| PD |
| EC |
| EP |
| PD |
| AS |
| FP |
| FA |
| CR |
| AS |
| EC•FP |
| EP•FA |
由①，②得
| BR•AS |
| DS•CR |
| EB•FA |
| EC•FD |
| BR |
| RC |
| CD |
| DS |
| SA |
| AB |
| EB |
| BA |
| AF |
| FD |
| DC |
| CE |
对△EAD应用梅涅劳斯定理，有
| EB |
| BA |
| AF |
| FD |
| DC |
| CE |
由③，④得
| BR |
| RC |
| CD |
| DS |
| SA |
| AB |
∴BD，RS，AC交于一点，
所以R，T，S三点共线．
点评：本题考查了三角形相似的判定与性质：有两个角对应相等的两个三角形相似；相似三角形的对应边的比相等．也考查了梅涅劳斯定理及其引理以及比例的性质．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
若k=
=
=
（a+b+c≠0），则k的值为（ ）
| 2a+b |
| c |
| 2c+a |
| b |
| 2b+c |
| a |
| A、1 | B、2 | C、3 | D、非上述答案 |
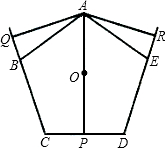如图，ABCDE是正五边形，从顶点A向三边BC、CD、DE（或其延长线）作垂线AQ、AP、AR、（Q、P、R是垂足），O是此五边形的中心，若OP=1，求AO+AQ+AR的值．