题目内容
18.解下列的一元一次不等式,并把解集在数轴上表示(1)$\frac{x}{2}$>$\frac{x}{3}$;
(2)$\frac{x-1}{7}$<$\frac{2x-2}{3}$;
(3)$\frac{2x+1}{2}$-$\frac{x-2}{3}$>1.
分析 (1)先去分母,再移项,合并同类项,再把解集再数轴上表示出来即可;
(2)、(3)先去分母,再去括号,移项,合并同类项,把x的系数化为1,再把解集再数轴上表示出来即可.
解答 解:(1)去分母得,3x>2x,
移项得,3x-2x>0,
合并同类项得,x>0.
在数轴上表示为: ;
;
(2)去分母得,3(x-1)<7(2x-2),
去括号得,3x-3<14x-14,
移项得,3x-14x<-14+3,
合并同类项得,-11x<-11,
x的系数化为1得,x>1.
在数轴上表示为: ;
;
(3)去分母得,3(2x+1)-2(x-2)>6,
去括号得,6x+3-2x+4>6,
移项得,6x-2x>6-3-4,
合并同类项得,4x>-1,
x的系数化为1得,x>-$\frac{1}{4}$.
在数轴上表示为: .
.
点评 本题考查的是解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
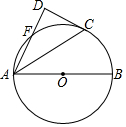 如图.⊙O的半径为5,AB为⊙O直径,C,F为⊙O上的两点,AF,AC为⊙O的弦.
如图.⊙O的半径为5,AB为⊙O直径,C,F为⊙O上的两点,AF,AC为⊙O的弦.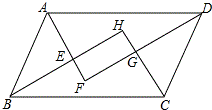 如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形.
如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形.